Bài 5 trang 148 SGK Đại số 10

Tính \(α\), biết:

LG a

\(\cosα = 1\);

Phương pháp giải:

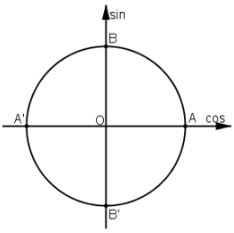
Dựa vào đường tròn lượng giác.

Lời giải chi tiết:

\(\cos \alpha  = 1 \Leftrightarrow M \equiv A\)  \( \Leftrightarrow \alpha  = k2\pi ,k \in \mathbb{Z}\)

LG b

\(\cosα = -1\)

Lời giải chi tiết:

\(\cos \alpha  =  - 1 \) \(\Leftrightarrow M \equiv A' \) \(\Leftrightarrow \alpha  = \pi  + k2\pi  = \left( {2k + 1} \right)\pi ,k \in Z\)

LG c

\(\cosα = 0\);

Lời giải chi tiết:

\(\cos \alpha  = 0 \Leftrightarrow \left[ \begin{array}{l}M \equiv B\\M \equiv B'\end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}\alpha  = \dfrac{\pi }{2} + m2\pi \\\alpha  =  - \dfrac{\pi }{2} + n2\pi \end{array} \right.\) \( \Leftrightarrow \alpha  = \dfrac{\pi }{2} + k\pi ,k \in \mathbb{Z}\)

LG d

\(\sinα = 1\)

Lời giải chi tiết:

\(\sin \alpha  = 1 \Leftrightarrow M \equiv B \) \(\Leftrightarrow \alpha  = \dfrac{\pi }{2} + k2\pi,k \in\mathbb Z \)

LG e

\(\sinα = -1\);

Lời giải chi tiết:

\(\sin \alpha  =  - 1 \Leftrightarrow M \equiv B' \) \(\Leftrightarrow \alpha  =  - \dfrac{\pi }{2} + k2\pi , k \in\mathbb Z\)

LG f

\(\sinα = 0\),

Lời giải chi tiết:

\(\sin \alpha  = 0\) \( \Leftrightarrow \left[ \begin{array}{l}M \equiv A\\M \equiv A'\end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}\alpha  = m2\pi \\\alpha  = \left( {2n + 1} \right)\pi \end{array} \right.\) \( \Leftrightarrow \alpha  = k\pi ,k \in\mathbb Z\)