Bài 5 trang 100 SGK Toán 11 tập 1 - Cánh diều
Cho hình chóp S.ABCD có đáy ABCD là hình thang với AB là đáy lớn và \(AB = 2CD\).Gọi M, N lần lượt là trung điểm của các cạnh SA và SB. Chứng minh rằng đường thẳng NC song song với đường thẳng MD.
Đề bài
Cho hình chóp S.ABCD có đáy ABCD là hình thang với AB là đáy lớn và \(AB = 2CD\).Gọi M, N lần lượt là trung điểm của các cạnh SA và SB. Chứng minh rằng đường thẳng NC song song với đường thẳng MD.
Phương pháp giải - Xem chi tiết
Hình bình hành là hình có các cặp cạnh đối song song và bằng nhau.
Đường trung bình của tam giác là đường đi qua trung điểm 2 cạnh, đường trung bình song song với đáy và bằng nửa cạnh đáy.
Lời giải chi tiết
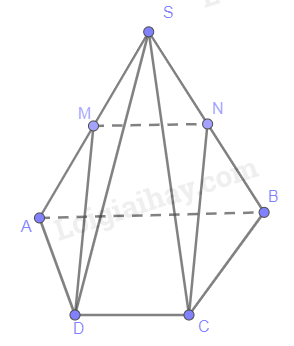
Ta có:MN là đường trung bình của tam giác SAB \(\Rightarrow MN//AB, MN= \frac{1}{2}AB \)
Mà \(\ CD//AB, CD= \frac{1}{2}AB \)
Suy ra: MN//CD, MN = CD.
Từ (1) và (2) suy ra MNCD là hình bình hành
Vậy NC // MD.
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 5 trang 100 SGK Toán 11 tập 1 - Cánh diều timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 5 trang 100 SGK Toán 11 tập 1 - Cánh diều timdapan.com"







