Bài 3 trang 77 SGK Hình học 11

Đề bài

Cho hình chóp đỉnh \(S\) có đáy là hình thang \(ABCD\) với \(AB\) là đáy lớn. Gọi \(M, N\) theo thứ tự là trung điểm của các cạnh \(SB, SC\)

a) Tìm giao tuyến của hai mặt phẳng \((SAD)\) và \((SBC)\)

b) Tìm giao điểm của đường thẳng \(SD\) với mặt phẳng \((AMN)\)

c) Tìm thiết dện của hình chóp \(S.ABCD\) cắt bởi mặt phẳng \((AMN)\)

Lời giải chi tiết

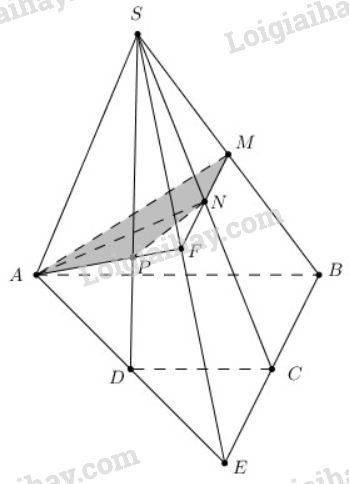
a) Trong \((ABCD)\) gọi \(E=AD\cap BC\)

\( \Rightarrow \left\{ \begin{array}{l}E \in AD \subset \left( {SAD} \right)\\E \in BC \subset \left( {SBC} \right)\end{array} \right.\) \( \Rightarrow E \in \left( {SAD} \right) \cap \left( {SBC} \right)\).

Mà \(S \in \left( {SAD} \right) \cap \left( {SBC} \right)\) \( \Rightarrow SE = \left( {SAD} \right) \cap \left( {SBC} \right)\).

b) Trong \((SBE)\): gọi \(F=MN ∩ SE\) \( \Rightarrow F \in SE \subset \left( {SAE} \right)\).

Trong \((SAE)\): gọi \(P= AF ∩ SD\) 

\( \Rightarrow P \in AF \subset \left( {AMN} \right)\). Mà \(P \in SD\) nên \(P=SD\cap (AMN)\)

c) Ta có: \(\left( {AMN} \right) \cap \left( {SAD} \right) = AP\)

+) \(\left( {AMN} \right) \cap \left( {SCD} \right) = PN\)

+) \(\left( {AMN} \right) \cap \left( {SBC} \right) = MN\)

+) \(\left( {AMN} \right) \cap \left( {SAB} \right) = AM\)

Vậy thiết diện của hình chóp cắt bởi mặt phẳng \((AMN)\) là tứ giác \(AMNP\).