Giải mục 1 trang 6, 7 ,8 SGK Toán 11 tập 1 - Kết nối tri thức

Hoạt động 1

Trên đồng hồ ở Hình 1.2, kim phút đang chỉ đúng số 2.

a) Phải quay kim phút mấy phần của một vòng tròn theo chiều quay ngược chiều kim đồng hồ để nó chỉ đúng số 12?

b) Phải quay kim phút mấy phần của một vòng tròn theo chiều quay của kim đồng hồ để nó chỉ đúng số 12?

c) Có bao nhiêu cách quay kim phút theo một chiều xác định để kim phút từ vị trí chỉ đúng số 2 về vị trí chỉ đúng số 12?

Phương pháp giải:

Đồng hồ được chia thành từng phần theo các số, kim phút đi qua bao nhiêu số thì quay bấy nhiêu phần của vòng tròn.

Lời giải chi tiết:

a) Khi kim phút quay theo ngược chiều kim đồng hồ để nó chỉ đúng số 12, kim phút quay:

 \(\frac{2}{{12}} = \frac{1}{6}\) phần của vòng tròn

b) Khi kim phút quay theo đúng chiều kim đồng hồ để nó chỉ đúng số 12, kim phút quay:

\(\frac{{10}}{{12}} = \frac{5}{6}\) phần của vòng tròn

c) Có 2 cách quay kim phút theo một chiều xác định để kim phút từ vị trí chỉ đúng số 2 về vị trí chỉ đúng số 12, đó là: ngược chiều kim đồng hồ và cùng chiều kim đồng hồ

Luyện tập 1

Cho góc hình học  \(\widehat {uOv} = {45^0}\). Xác định số đo của góc lượng giác \((Ou,Ov)\) trong mỗi trường hợp sau:

Phương pháp giải:

Mỗi góc lượng giác gốc O được xác định bởi tia đầu Ou, tia cuối Ov và số đo của nó.

Lời giải chi tiết:

a) Ta có:

- Các góc lượng giác tia đầu Ou, tia cuối Ov có số đo là \((Ou,Ov) = {45^ \circ } + k{.360^ \circ }\)

b) Ta có:

- Các góc lượng giác tia đầu Ou, tia cuối Ov có số đo là \((Ou,Ov) =  - {315^ \circ } + k{.360^ \circ }\)

Hoạt động 2

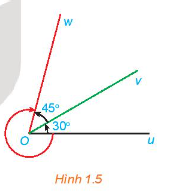
Cho ba tia Ou, Ov, Owvới số đo của các góc hình học uOv và vOw lần lượt là \({30^ \circ }\) và \({45^ \circ }\)

a) Xác định số đo của ba góc lượng giác \((Ou,Ov)\) ,\((Ov,Ow\) và \((Ou,Ow)\)  được chỉ ra ở Hình 1.5.

b) Với các góc lượng giác ở câu a, chứng tỏ rằng có một số nguyên k để

sđ\((Ou,Ov)\) + sđ\((Ov,Ow\) = sđ \((Ou,Ow)\) + k\({.360^ \circ }\)

Phương pháp giải:

Xác định các tia đầu, tia cuối và chiều quay để tìm được số đo của các góc lượng giác.

Lời giải chi tiết:

a) Ta có:

- Các góc lượng giác tia đầu Ou, tia cuối Ov có số đo là

sđ\((Ou,Ov) =  {30^ \circ } + n{.360^ \circ }\)

- Các góc lượng giác tia đầu Ov, tia cuối Ow có số đo là

sđ \((Ov,Ow) =  {45^ \circ } + m{.360^ \circ }\)

- Các góc lượng giác tia đầu Ou, tia cuối Ow có số đo là

sđ \((Ou,Ow) =  {75^ \circ } + k{.360^ \circ }\)

b) Với các góc lượng giác ở câu a, ta có:

\(sđ(Ou,Ov) +sđ (Ov,Ow)\)

\(  =  {30^ \circ } + n{.360^ \circ } + {45^ \circ } + m{.360^ \circ } \)

\(= {75^ \circ } + (n+m){.360^ \circ } \)

\(= {75^ \circ } + k{.360^ \circ = sđ (Ou,Ow)} \)

với  k = n + m

Luyện tập 2

Cho một góc lượng giác $(O x, O u)$ có số đo $240^{\circ}$ và một góc lượng giác $(O x, O v)$ có số đo $-270^{\circ}$. Tính số đo của các góc lượng giác $(O u, O v)$.

Phương pháp giải:

Áp dụng hệ thức Charles: Với ba tia tùy ý \(O x, O u, O v \), ta có:

sđ\((Ou,Ov)\) = sđ\((Ox,Ov)\) - sđ \((Ox,Ou)\) + k\({.360^ \circ }\)

Lời giải chi tiết:

Số đo của các góc lượng giác tia đầu $O u$, tia cuối $O v$ là

\(sđ(O u, O v) = sđ(O x, O v)  -  sđ(O x, O u)+ k{360}^{\circ}(k \in \mathbb{Z}) \)

\(=-270^{\circ}-240^{\circ}+k 360^{\circ}=-510^{\circ}+k 360^{\circ} \)
\( =-150^{\circ}+(k-1) 360^{\circ}=-150^{\circ}+n 360^{\circ} \quad(n=k-1, n \in \mathbb{Z})
\)
Vậy các góc lượng giác $(O u, O v)$ có số đo là $-150^{\circ}+n 360^{\circ} \quad(n \in \mathbb{Z})$.