Giải bài tập 1 trang 72 SGK Toán 9 tập 1 - Chân trời sáng tạo
Cho tam giác ABC vuông tại A có AC = 10 cm, \(\widehat C = {60^o}\). Độ dài hai cạnh còn lại là: A. \(AB = \frac{{5\sqrt 3 }}{3}cm;BC = \frac{{20\sqrt 3 }}{3}cm\) B. \(AB = \frac{{10\sqrt 3 }}{3}cm;BC = \frac{{14\sqrt 3 }}{3}cm\) C. \(AB = 10\sqrt 3 cm;BC = 20cm\) D. \(AB = \frac{{10\sqrt 3 }}{3}cm;BC = \frac{{20\sqrt 3 }}{3}cm\)
Đề bài
Cho tam giác ABC vuông tại A có AC = 10 cm, \(\widehat C = {60^o}\). Độ dài hai cạnh còn lại là:
A. \(AB = \frac{{5\sqrt 3 }}{3}cm;BC = \frac{{20\sqrt 3 }}{3}cm\)
B. \(AB = \frac{{10\sqrt 3 }}{3}cm;BC = \frac{{14\sqrt 3 }}{3}cm\)
C. \(AB = 10\sqrt 3 cm;BC = 20cm\)
D. \(AB = \frac{{10\sqrt 3 }}{3}cm;BC = \frac{{20\sqrt 3 }}{3}cm\)
Phương pháp giải - Xem chi tiết
Đọc kĩ dữ liệu đề bài để vẽ hình
Dựa vào định lí: Xét tam giác vuông :
+ Mỗi cạnh góc vuông bằng cạnh huyền nhân sin góc đối hoặc nhân côsin góc kề rồi suy ra cạnh góc vuông.
+ Áp dụng định lý Pythagore trong tam giác vuông tìm cạnh góc vuông còn lại.
Lời giải chi tiết
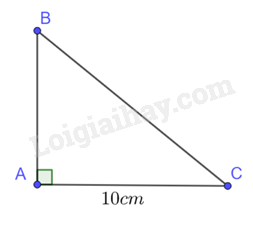
Xét tam giác ABC vuông tại A, \(\widehat C = {60^o}\), ta có:
AB = tan\(\widehat C\). AC = tan\({60^o}\). 10 = 10\(\sqrt 3 \) cm
BC = \(\frac{{AC}}{{\sin \widehat C}} = \frac{{10}}{{\sin {{60}^o}}} = \frac{{20\sqrt 3 }}{3}\)cm.
Không có đáp án đúng.
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài tập 1 trang 72 SGK Toán 9 tập 1 - Chân trời sáng tạo timdapan.com"







