Bài 78 trang 148 SBT toán 7 tập 1

Đề bài

Cho tam giác \(ABC.\) Các tia phân giác của các góc \(B\) và \(C\) cắt nhau ở \(I.\) Qua \(I\) kẻ đường thẳng song song với \(BC.\) Gọi giao điểm của đường thẳng này với \(AB, AC\) theo thứ tự là \(D, E.\) Chứng minh rằng \( DE = BD + CE.\)

Lời giải chi tiết

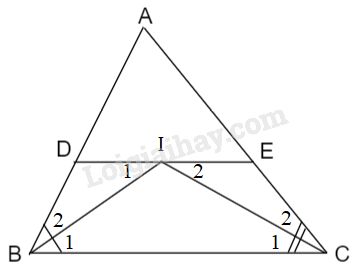
Vì \(DI // BC\) (gt)

\( \Rightarrow \widehat {{I_1}} = \widehat {{B_1}}\) (hai góc so le trong)       (1)

Lại có: \({\widehat B_1} = \widehat {{B_2}}\) (vì \(BI\) là tia phân giác của \(\widehat B\))           (2)

Từ (1) và (2) suy ra: \(\widehat {{I_1}} = \widehat {{B_2}}\)

\( \Rightarrow  ∆BDI\) cân tại \(D\) \( \Rightarrow BD = DI  \)               (3)

Vì \(IE // BC\) (gt) \( \Rightarrow \widehat {{I_2}} = \widehat {{C_1}}\) (hai góc so le trong)              (4)

Lại có: \(\widehat {{C_1}} = \widehat {{C_2}}\) (vì \(CI\) là tia phân giác của \(\widehat {{C}}\))        (5)

Từ (4) và (5) suy ra: \(\widehat {{I_2}} = \widehat {{C_2}}\)

\( \Rightarrow ∆CEI\) cân tại \(E\) \( \Rightarrow  CE = EI\)                   (6)     

Từ (3) và (6) suy ra: \(BD + CE = DI + EI = DE.\)