Bài 76 trang 147 SBT toán 7 tập 1
Giải bài 76 trang 147 sách bài tập toán 7 tập 1. Cho tam giác ABC cân tại A có cạnh bên bằng 3cm...
Đề bài
Cho tam giác \(ABC\) cân tại \(A\) có cạnh bên bằng \(3cm.\) Gọi \(D\) là một điểm thuộc đáy \(BC.\) Qua \(D,\) kẻ các đường thẳng song song với các cạnh bên, chúng cắt \(AB\) và \(AC\) theo thứ tự tại \(F\) và \(E.\) Tính tổng \(DE + DF.\)
Phương pháp giải - Xem chi tiết
- Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.
- Tam giác cân có hai cạnh bên bằng nhau, hai góc đáy bằng nhau.
Lời giải chi tiết
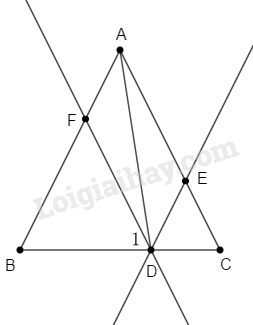
Vì \(DF // AC\) (gt) \( \Rightarrow \widehat {{D_1}} = \widehat C\) (hai góc đồng vị) (1)
Lại có \(∆ABC \) cân tại \(A\).
\( \Rightarrow \widehat B = \widehat C\) (tính chất tam giác cân) (2)
Từ (1) và (2) suy ra \(\widehat B = \widehat {{D_1}}\) do đó \(∆BFD\) cân tại \(F\).
\( \Rightarrow BF = DF\) (tính chất tam giác cân).
Nối \(AD\).
Vì \(DF//AC\) nên \(\widehat {A{\rm{D}}F} = \widehat {D{\rm{AE}}}\) (hai góc so le trong).
Vì \(DE//AB\) nên \(\widehat {FAD} = \widehat {E{\rm{D}}A}\) (hai góc so le trong).
Xét \(∆AFD\) và \( ∆DEA\) có:
\(\widehat {A{\rm{D}}F} = \widehat {D{\rm{AE}}}\) (chứng minh trên)
\(AD\) cạnh chung
\(\widehat {FAD} = \widehat {E{\rm{D}}A}\) (chứng minh trên)
\( \Rightarrow ∆AFD = ∆DEA\) (g.c.g)
\( \Rightarrow AF = DE\) (hai cạnh tương ứng).
Vậy \(DE + DF = AF + BF = AB \)\(\,= 3\,(cm)\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 76 trang 147 SBT toán 7 tập 1 timdapan.com"







