Giải Bài 70 trang 89 sách bài tập toán 7 - Cánh diều

Đề bài

Cho tam giác ABC cân tại A có hai trung tuyến BM và CN cắt nhau tại G. Chứng minh:

a) BM = CN;

b) Tam giác GBC là tam giác cân;

c) AG vuông góc với BC.

Lời giải chi tiết

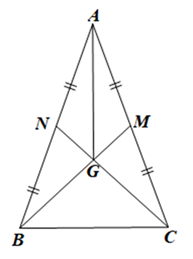
a) Vì tam giác ABC cân tại A nên AB = AC, \(\widehat {ABC} = \widehat {ACB}\).

Vì BM, CN là đường trung tuyến của tam giác ABC nên M, N lần lượt là trung điểm của AC và AB.

Do đó AM = MC, AN = NB.

Mà AB = AC

Suy ra AM = MC = AN = NB.

Xét ∆ABM và ∆ACN có:

AB = AC (chứng minh trên),

\(\widehat {BAC}\) là góc chung,

AM = AN (chứng minh trên)

Do đó ∆ABM = ∆ACN (c.g.c).

Suy ra BM = CN (hai cạnh tương ứng).

Vậy BM = CN.

b) Do ∆AMB = ∆ANC (câu a) suy ra \(\widehat {ABM} = \widehat {ACN}\) (hai góc tương ứng).

Ta có \(\widehat {ACB} = \widehat {ACN} + \widehat {NCB}\), .

Mà \(\widehat {ABC} = \widehat {ACB}\) và \(\widehat {ABM} = \widehat {ACN}\).

Nên \(\widehat {MBC} = \widehat {NCB}\) hay \(\widehat {GBC} = \widehat {GCB}\).

Suy ra tam giác GBC cân tại G.

Vậy tam giác GBC cân tại G

c) Ta có AB = AC nên A nằm trên đường trung trực của đoạn thẳng BC.

Theo câu b tam giác GBC cân tại G nên GB = GC (hai cạnh bên).

Do đó G nằm trên trung trực của đoạn thẳng BC.

Suy ra AG là đường trung trực của đoạn thẳng BC nên AG vuông góc với BC tại trung điểm của BC.

Vậy AG vuông góc với BC.