Bài 63 trang 115 SBT toán 9 tập 1

Đề bài

Cho tam giác \(ABC\) có \(BC = 12cm\), \(\widehat B = 60^\circ ,\widehat C = 40^\circ .\) Tính:

a)  Đường cao \(CH\) và cạnh \(AC;\)

b)  Diện tích tam giác \(ABC.\)  

Lời giải chi tiết

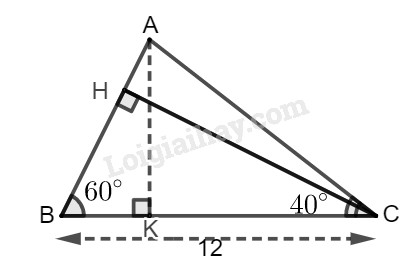
a) Trong tam giác vuông BCH, ta có:

\(CH = BC.\sin \widehat B\)\( = 12.\sin 60^\circ  \approx 10,392\) (cm)

Trong tam giác ABC, ta có:

\(\widehat A = 180^\circ  - (60^\circ  + 40^\circ ) = 80^\circ \)

Trong tam giác vuông ACH, ta có:

\(AC = \dfrac{{CH}}{{\sin \widehat A}}\)\( \approx \dfrac{{10,392}}{{\sin 80^\circ }} = 10,552\) (cm)

b) Kẻ \(AK \bot BC\)

Trong tam giác vuông ACK, ta có:

\(AK = AC.\sin \widehat C\)\( \approx 10,552.\sin 40^\circ  = 6,783\) (cm)

Vậy \({S_{ABC}} = \dfrac{1}{ 2}.AK.BC\)\( \approx \dfrac {1}{ 2}.6,783.12 = 40,696\) (cm²)