Bài 53 trang 113 SBT toán 9 tập 1

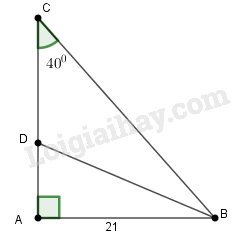
Đề bài

Tam giác \(ABC\) vuông tại \(A\) có \(AB = 21cm\), \(\widehat C = 40^\circ \). Hãy tính các độ dài:

a) \(AC\) ;                  b) \(BC\) ;

c) Phân giác \(BD.\)  

Lời giải chi tiết

a) Ta có: \(AC = AB.\cot g\widehat C\)\( = 21.\cot g40^\circ  \approx 25,0268\left( {cm} \right)\)

b) Ta có: \(BC = \dfrac{{AC}}{{\sin \widehat C}} = \dfrac{{21}}{{\sin 40^\circ }}\)\( \approx 32,6702\left( {cm} \right)\) 

c) Vì \(\Delta ABC\) vuông tại \(A\) nên \(\widehat B + \widehat C = 90^\circ \)

Suy ra: \(\widehat B = 90^\circ  - \widehat C = 90^\circ  - 40^\circ  = 50^\circ \)

Vì \(BD\) là phân giác của góc \(B\) nên: 

\(\widehat {ABD} = \dfrac{1}{ 2}\widehat B = \dfrac{1 }{2}.50^\circ  = 25^\circ \) 

Trong  tam giác vuông \(ABD\), ta có:

\(BD = \dfrac{{AB}}{{{\rm{cos}}\widehat {ABD}}} = \dfrac{{21}}{{\cos 25^\circ }}\)\( \approx 23,1709\left( {cm} \right)\)