Bài 1.64 trang 40 SBT hình học 11

Đề bài

Trong mặt phẳng \(Oxy\) cho điểm \(M\left( {1;1} \right)\). Ảnh của \(M\) qua phép quay tâm \(O\), góc quay \({45^0}\) có tọa độ

A. \(\left( { - 1;1} \right)\)                      B. \(\left( {1;0} \right)\)

C. \(\left( {\sqrt 2 ;0} \right)\)                   D. \(\left( {0;\sqrt 2 } \right)\)

Lời giải chi tiết

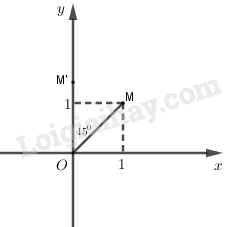
Dễ thấy \(M\left( {1;1} \right)\) nằm trên đường phân giác của góc phần tư thứ nhất.

Khi đó \(M' = {Q_{\left( {O,{{45}^0}} \right)}}\left( M \right)\) \( \Leftrightarrow \left( {OM,OM'} \right) = {45^0}\) nên \(M'\) nằm trên tia \(Oy\).

Do đó \(M'\left( {0;m} \right)\) với \(m > 0\).

Lại có \(OM = OM'\) \( \Leftrightarrow \sqrt 2  = \sqrt {0 + {m^2}}  \Leftrightarrow m = \sqrt 2 \).

Vậy \(M'\left( {0;\sqrt 2 } \right)\).

Chọn D.