Đề kiểm tra 15 phút - Đề số 8 - Bài 7, 8 - Chương 2 - Hình học 7

Đề bài

Cho tam giác ABC cân tại A. Kẻ qua B tia Bx vuông góc với AB, qua C kẻ tia Cy vuông góc với AC, gọi I là giao điểm của Bx và Cy.

a) Chứng minh \(\Delta ABI = \Delta ACI.\)

b) Chứng tỏ AI là đường trung trực của đoạn BC.

Lời giải chi tiết

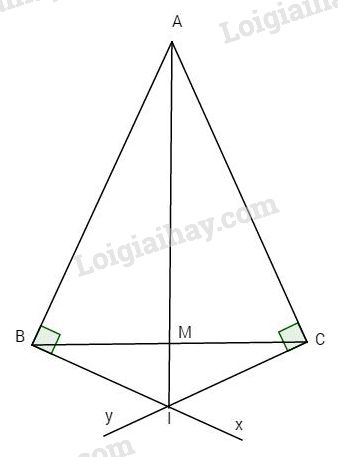
a) Ta có \(Bx \bot AB,\,Cy \bot AC.\)

Xét hai tam giác vuông ABI và ACI có:

+) AI cạnh chung,

+) \(AB = AC\) (giả thiết).

Do đó \(\Delta ABI = \Delta ACI\) (ch.cgv).

b) \(\Delta ABI = \Delta ACI\) (chứng minh trên)

\( \Rightarrow \widehat {BAI} = \widehat {CAI}\) (góc tương ứng).

Gọi M là giao điểm của AI và BC.

Xét \(\Delta AMB\) và \(\Delta AMC\) có:

+) AM cạnh chung;

+) \(\widehat {BAM} = \widehat {CAM}\) (chứng minh trên);

+) \(AB = AC\) (giả thiết).

Do đó \(\Delta AMB = \Delta AMC\) (c.g.c)

\( \Rightarrow MB = MC\,\;(1)\) và \(\widehat {AMB} = \widehat {AMC}\).

Mà \(\widehat {AMB} + \widehat {AMC} = {180^o}\) (kề bù)

\( \Rightarrow \widehat {AMB} = \widehat {AMC} = {90^o}\).

Chứng tỏ \(AM \bot BC\)  (2).

Từ (1) và (2) \( \Rightarrow AI\) là đường trung trực của BC.