Bài 1.18 trang 9 SBT Đại số và Giải tích 11 Nâng cao

Phép đối xứng qua điểm \(I\left( {{\pi  \over 2};0} \right)\) biến đồ thị mỗi hàm số sau thành đồ thị của hàm số nào? Vẽ đồ thị của hàm số tìm được.

LG a

\(y = \sin x\)

Phương pháp giải:

Điểm đối xứng của điểm \(M\left( {x;y} \right)\) qua điểm \(\left( {{\pi  \over 2};0} \right)\) là điểm \(M'\left( {x';y'} \right)\)

\(x' = \pi  - x;y' =  - y\) tức là \(x = \pi  - x',y =  - y'.\)

Lời giải chi tiết:

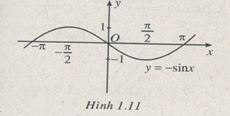
 \(y =  - \sin x\)

LG b

\(y = \cos 2x\)

Phương pháp giải:

Điểm đối xứng của điểm \(M\left( {x;y} \right)\) qua điểm \(\left( {{\pi  \over 2};0} \right)\) là điểm \(M'\left( {x';y'} \right)\)

\(x' = \pi  - x;y' =  - y\) tức là \(x = \pi  - x',y =  - y'.\)

Lời giải chi tiết:

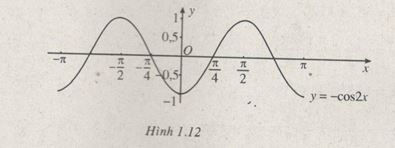
\(y =  - \cos 2x\) (h.1.12)

LG c

\(y = \sin {x \over 2}\)

Phương pháp giải:

Điểm đối xứng của điểm \(M\left( {x;y} \right)\) qua điểm \(\left( {{\pi  \over 2};0} \right)\) là điểm \(M'\left( {x';y'} \right)\)

\(x' = \pi  - x;y' =  - y\) tức là \(x = \pi  - x',y =  - y'.\)

Lời giải chi tiết:

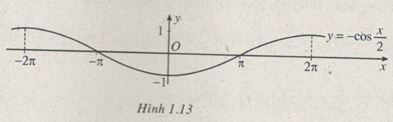
\(y =  - \cos {x \over 2}\) (h.1.13)