Bài 1 trang 34 SGK Hình học 10 Nâng cao
Cho tam giác ABC . Hãy xác định các vectơ
Đề bài
Cho tam giác \(ABC\) . Hãy xác định các vec tơ
\(\eqalign{
& \overrightarrow {AB} + \overrightarrow {BC} \,\,;\,\,\,\,\,\,\overrightarrow {CB} + \overrightarrow {BA} \,\,;\cr&\overrightarrow {AB} + \overrightarrow {CA} \,\,;\,\,\,\,\overrightarrow {BA} + \overrightarrow {CB} \,\,;\, \cr
& \overrightarrow {BA} + \overrightarrow {CA} \,\,;\,\,\,\,\,\,\,\overrightarrow {CB} - \overrightarrow {CA} \cr&\overrightarrow {AB} - \overrightarrow {CB} \,\,;\,\,\,\,\overrightarrow {BC} - \overrightarrow {AB} \,\,.\, \cr} \)
Phương pháp giải - Xem chi tiết
Sử dụng quy tắc ba điểm và quy tắc hình bình hành:
\(\begin{array}{l}
\overrightarrow {MN} + \overrightarrow {NP} = \overrightarrow {MP} \\
\overrightarrow {MN} = \overrightarrow {PN} - \overrightarrow {PM} \\
\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC}
\end{array}\)
Ở đố M, N, P là ba điểm bất kì, ABCD là hình bình hành.
Lời giải chi tiết
Ta có
\(\eqalign{
& \overrightarrow {AB} + \overrightarrow {BC} \,\, = \overrightarrow {AC} \,\,\,\,\, \cr
& \overrightarrow {CB} + \overrightarrow {BA} \,\, = \overrightarrow {CA} \,\,\,\,\,\,\,\,\,\, \cr
& \overrightarrow {AB} + \overrightarrow {CA} \,\, = \,\overrightarrow {CA} \, + \,\overrightarrow {AB} \, = \,\overrightarrow {CB} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \cr
& \overrightarrow {BA} + \overrightarrow {CB} \,\, = \overrightarrow {CB} + \overrightarrow {BA} = \overrightarrow {CA} \cr} \)
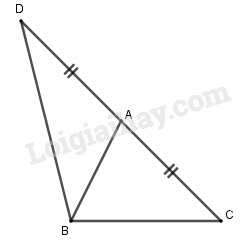
\(\overrightarrow {BA} + \overrightarrow {CA} = \overrightarrow {BA} + \overrightarrow {AD} = \overrightarrow {BD} \)
(Với \(D\) thỏa mãn \(\overrightarrow {CA} = \overrightarrow {AD} \), tức \(D\) là điểm đối xứng với \(C\) qua \(A\)).
\(\eqalign{
& \overrightarrow {CB} - \overrightarrow {CA} = \overrightarrow {AB} \cr
& \overrightarrow {AB} - \overrightarrow {CB} = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \cr} \)
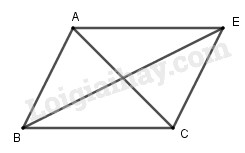
\(\overrightarrow {BC} - \overrightarrow {AB} = \overrightarrow {BC} + \overrightarrow {BA} = \overrightarrow {BE} \)
(Với \(E\) là điểm sao cho \(ABCE\) là hình bình hành).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 1 trang 34 SGK Hình học 10 Nâng cao timdapan.com"