Bài 1 trang 105 SGK Đại số 10

Xét dấu các tam thức bậc hai

LG a

\({5x^{2}}-3x + 1\); 

Phương pháp giải:

Cho đa thức bậc hai: \(f\left( x \right) = a{x^2} + bx + c\;\;\left( {a \ne 0} \right),\;\;\)\(\Delta  = {b^2} - 4ac.\)

+) Nếu \(\Delta < 0\) thì \(f(x)\) luôn cùng dấu với hệ số \(a,\) với mọi \(x \in R.\)

+) Nếu \(\Delta = 0\) thì \(f(x)\) luôn cùng dấu với hệ số \(a,\) trừ khi \(x=-\frac{b}{2a}.\)

+) Nếu \(\Delta > 0\) thì \(f(x)\) luôn cùng dấu với hệ số \(a\) khi \(x < x_1\) hoặc \(x > x_2,\) trái dấu với hệ số \(a\) khi \(x_1 < x < x_2\) trong đó \(x_1, \, \, x_2 \, \, (x_1 < x_2)\) là hai nghiệm của \(f(x).\)

Lời giải chi tiết:

\({5x^{2}}-3x + 1\)

\(∆ = (- 3)^2– 4.5 =-11< 0  \) nên luôn cùng dấu với \(a=5 > 0\).

\(\Rightarrow   5x^2- 3x + 1 > 0  , ∀x ∈\mathbb R\)

LG b

\(- 2{x^2} + 3x + 5\);

Lời giải chi tiết:

Tam thức bậc hai \(- 2{x^2} + 3x + 5\) có hệ số \(a=-2<0\).

Ta có: \( - 2{x^2} + 3x + 5=0 \Leftrightarrow \left[ \matrix{
x = - 1 \hfill \cr 
x = {5 \over 2} \hfill \cr} \right.\)

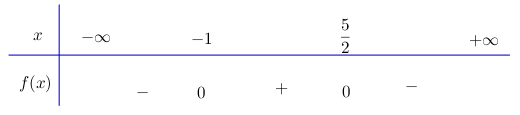
Ta có bảng xét dấu:

Vậy \( - 2{x^2} + 3x + 5 <0\)  với  \(x < -1\) hoặc \(x > \dfrac{5}{2}.\)

\( - 2{x^2} + 3x + 5 >0\) với   \(- 1 < x < \dfrac{5}{2}.\)

\(- 2{x^2} + 3x + 5 = 0 \) với \(x = -1\) hoặc \(x = \dfrac{5}{2}.\)

LG c

\({x^2} +12x+36\); 

Lời giải chi tiết:

\({x^2} +12x+36\)

Ta có: \(\Delta ' = {6^2} - 1.36 = 0\)

\({x^2} + 12x + 36 = 0 \Leftrightarrow x =  - 6\)

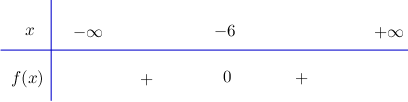
Ta có bảng xét dấu:

Vậy \({x^2} + 12x + 36 > 0, ∀x ≠ - 6.\)

LG d

\((2x - 3)(x + 5)\).

Lời giải chi tiết:

\((2x - 3)(x + 5)=2x^2+7x-15\)

\((2x - 3)(x + 5) = 0 \Leftrightarrow \left[ \matrix{
x = - 5 \hfill \cr 
x = {3 \over 2} \hfill \cr} \right.\)

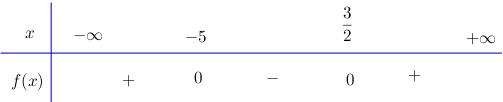
Ta có bảng xét dấu:

Vậy \((2x - 3)(x + 5) > 0\) với \(x < -5\) hoặc \(x > \dfrac{3}{2}.\)

\((2x - 3)(x + 5) < 0\) với \( -5 < x < \dfrac{3}{2}.\)

\((2x - 3)(x + 5) = 0\) với \(x = -5\) hoặc \(x = \dfrac{3}{2}.\)