Đề cương ôn tập học kì 2 môn Toán lớp 7 năm 2021 - 2022 là tài liệu ôn thi hay, giúp các em học sinh hệ thống toàn bộ kiến thức được học trong học kì 2 Toán 7. Tài liệu bao gồm các dạng Toán trọng tâm, các dạng đề thi mẫu chọn lọc dành cho các bạn học sinh lớp 7, giúp các bạn ôn tập lại lý thuyết và luyện tập các dạng bài khác nhau để chuẩn bị cho bài thi học kì 2 sắp tới. Đây đều là các nội dung quan trọng trong năm học, giúp các em học sinh củng cố kiến thức đã học và trau dồi thêm kỹ năng giải toán một cách chính xác và khoa học nhất. Sau đây mời các bạn tham khảo tải về bản đầy đủ.

I. Lý thuyết ôn tập Toán 7 học kì 2

Phần đại số 7

1. Dấu hiệu điều tra, tần số, công thức tính số TB cộng

2. Vẽ biểu đồ đoạn thẳng (cột, hình chữ nhật)

3. Biểu thức đại số, giá trị biểu thức đại số

4. Đơn thức là gì? Bậc của đơn thức, thế nào là hai đơn thức đồng dạng? Tính tích tổng các đơn thức đồng dạng

5. Đa thức là gì? Bậc của đa thức, thu gọn đa thức

6. Đa thức 1 biến là gì? Thu gọn, sắp xếp đa thức 1 biến? Tính tổng hiệu đa thức 1 biến

7. Nghiệm của đa thức 1 biến là gì? Khi nào 1 số được gọi là nghiệm của đa thức 1 biến? Cách tìm nghiệm của đa thức 1 biến

Phần Hình học 7

1. Các trường hợp bằng nhau của hai tam giác

2. Tam giác cân, tam giác đều

3. Định lý pitago

4. Quan hệ cạnh góc trong tam giác, hình chiếu và đường xiên, bất đẳng thức trong tam giác

5. Tính chất 3 đường trung tuyến

6. Tính chất phân giác của góc, tính chất 3 đường phân giác tròn tam giác

7. Tính chất 3 đường trung trực của tam giác

8. Tính chất 3 đường cao trong tam giác

II. Bài tập Toán lớp 7 học kì 2

A. Thống kê

Câu 1. Điểm kiểm tra toán học kỳ I của học sinh lớp 7A được ghi lại như sau:

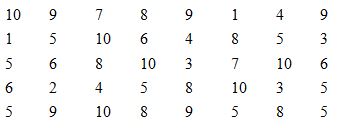
a) Dấu hiệu cần tìm ở đây là gì?

b) Lập bảng tần số và tính số trung bình cộng.

c) Tìm mốt của dấu hiệu.

d) Dựng biểu đồ đoạn thẳng (trục hoành biểu diễn điểm số; trục tung biểu diễn tần số).

Câu 2. Một GV theo dõi thời gian làm bài tập (thời gian tính theo phút) của 30 HS của một trường (ai cũng làm được) người ta lập bảng sau:

Thời gian (x)	5	7	8	9	10	14
Tần số (n)	4	3	8	8	4	3	N = 30

a) Dấu hiệu là gì? Tính mốt của dấu hiệu?

b) Tính thời gian trung bình làm bài tập của 30 học sinh?

c) Nhận xét thời gian làm bài tập của học sinh so với thời gian trung bình.

Câu 3. Số HS giỏi của mỗi lớp trong khối 7 được ghi lại như sau:

Lớp	7A	7B	7C	7D	7E	7G	7H
Số HS giỏi	32	28	32	35	28	26	28

a) Dấu hiệu ở đây là gì? Cho biết đơn vị điều tra.

b) Lập bảng tần số và nhận xét.

c) Vẽ biểu đồ đoạn thẳng.

Câu 4.: Tổng số điểm 4 môn thi của các học sinh trong một phòng thi được cho trong bảng dưới đây.

32	30	22	30	30	22	31	35
35	19	28	22	30	39	32	30
30	30	31	28	35	30	22	28

a/ Dấu hiệu ở đây là gì? Số tất cả các giá trị là bao nhiêu? số GT khác nhau của dấu hiệu?

b/ Lập bảng tần số, rút ra nhận xét

c/ Tính trung bình cộng của dấu hiệu, và tìm mốt

Câu 5: Lớp 7A góp tiền ủng hộ đồng bào bị thiên tai. Số tiền góp của mỗi bạn được thống kê trong bảng ( đơn vị là nghìn đồng)

1	2	1	4	2	5	2	3	4	1	5	2
3	5	2	2	4	1	3	3	2	4	2	3
4	2	3	10	5	3	2	1	5	3	2	2

a/ Dấu hiệu ở đây là gì?

b/ Lập bảng “tần số”, tính trung bình cộng

Câu 6. Thời gian làm bài tập của các hs lớp 7 tính bằng phút đươc thống kê bởi bảng sau:

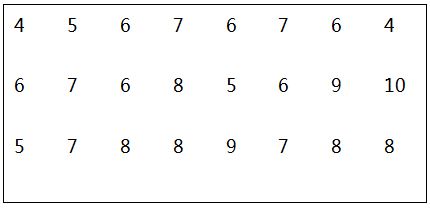
a. Dấu hiệu ở đây là gì? Số các giá trị là bao nhiêu?

b. Lập bảng tần số? Tìm mốt của dấu hiệu? Tính số trung bình cộng?

c. Vẽ biểu đồ đoạn thẳng?

Câu 7. Số cơn bão hàng năm đổ bộ vào lãnh thổ Việt Nam trong 20 năm cuối cùng của thế kỷ XX được ghi lại trong bảng sau:

3	3	6	6	3	5	4	3	9	8
2	4	3	4	3	4	3	5	2	2

a/ Dấu hiệu ở đây là gì?

b/ Lập bảng “tần số” và tính xem trong vòng 20 năm, mỗi năm trung bình có bao nhiêu cơn bão đổ bộ vào nước ta? Tìm mốt

c/ Biểu diễn bằng biểu đồ đoạn thẳng bảng tần số nói trên.

B. Đơn, đa thức

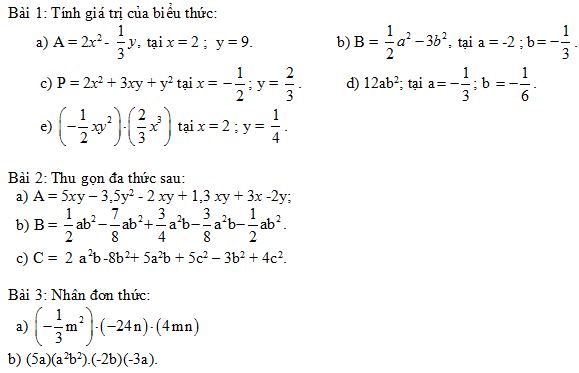
Bài 4: Tính tổng của các đa thức:

A = x²y - xy² + 3 x² và B = x²y + xy² - 2 x² - 1.

Bài 5: Cho P = 2x² – 3xy + 4y² ; Q = 3x² + 4 xy - y² ; R = x² + 2xy + 3 y².

Tính: P – Q + R.

Bài 6: Cho hai đa thức: M = 3,5x²y – 2xy² + 1,5 x²y + 2 xy + 3 xy²

N = 2 x²y + 3,2 xy + xy² - 4 xy² – 1,2 xy.

a) Thu gọn các đa thức M và N.

b) Tính M – N.

Bài 7: Tìm tổng và hiệu của: P(x) = 3x² +x - 4 ; Q(x) = -5 x² +x + 3.

Bài 8: Tính tổng các hệ số của tổng hai đa thức:

K(x) = x³ – mx + m² ; L(x) =(m + 1) x² +3m x + m².

Câu 9. Cho f(x) = (x – 4) – 3(x + 1). Tìm x sao cho f(x) = 4.

Bài 10: Tìm nghiệm của đa thức:

a) g(x) = (6 - 3x)(-2x+ 5); b) h(x) = x² + x.

Câu 11. Cho f(x) = 9 – x⁵ + 4 x - 2 x³ + x² – 7 x⁴;

g(x) = x⁵ – 9 + 2 x² + 7 x⁴ + 2 x³ - 3 x.

a) Sắp xếp các đa thức trên theo lũy thừa giảm dần của biến.

b) Tính tổng h(x) = f(x) + g(x).

c) Tìm nghiệm của đa thức h(x).

Câu 12. Cho các đa thức: f(x) = x³ - 2x² + 3x + 1

g(x) = x³ + x - 1

h(x) = 2x2 - 1

a) Tính: f(x) - g(x) + h(x)

b) Tìm x sao cho f(x) - g(x) + h(x) = 0

Câu 13.

Cho P(x) = x³ - 2x + 1 ; Q(x) = 2x² – 2x³ + x - 5.

Tính a) P(x) + Q(x); b) P(x)-Q(x)

Câu 14: Cho hai đa thức:

A(x) = –4x⁵ – x³ + 4x² + 5x + 9 + 4x⁵ – 6x² – 2

B(x) = –3x⁴ – 2x³ + 10x² – 8x + 5x³ – 7 – 2x³ + 8x

a)Thu gọn mỗi đa thức trên rồi sắp xếp chúng theo lũy thừa giảm dần của biến

b) Tính P(x) = A(x) + B(x) và Q(x) = A(x) – B(x)

c) Chứng tỏ x = –1 là nghiệm của đa thức P(x).

Câu 15:

Cho f(x) = x³ − 2x + 1, g(x) = 2x² − x3 + x −3

a) Tính f(x) + g(x) ; f(x)−g(x).

b) Tính f(x) +g(x) tại x = – 1; x =-2

Câu 16:  Cho đa thức

M = x² + 5x⁴ − 3x³ + x² + 4x⁴ + 3x³ − x + 5

N = x − 5x³ − 2x² − 8x⁴ + 4x³ − x + 5

a. Thu gọn và sắp xếp các đa thức theo lũy thừa giảm dần của biến

b. Tính M + N; M- N

C. Hình học 7

Bài 1) Cho tam giác ABC có CA = CB = 10cm, AB = 12cm. Kẻ CI vuông góc với AB (I thuộc AB)

a) C/m rằng IA = IB

b) Tính độ dài IC.

c) Kẻ IH vuông góc với AC (H thuộc AC), kẻ IK vuông góc với BC (K thuộc BC).

So sánh các độ dài IH và IK.

Bài 2) Cho tam giác ABC cân tại A. Trên cạnh AB lấy điểm D. Trên cạnh AC lấy điểm E sao cho AD = AE

a) C/M rằng BE = CD.

b) C/M rằng góc ABE bằng góc ACD.

c) Gọi K là giao điểm của BE và CD. Tam giác KBC là tam giác gì? Vì sao?

Bài 3) Cho tam giác ABC vuông ở C, có góc A bằng 600. Tia phân giác của góc BAC cắt BC ở E. Kẻ EK vuông góc với AB (K thuộc AB). Kẻ BD vuông góc với tia AE (D thuộc tia AE). C/M:

a) AC = AK và AE vuông góc CK.

b) KA = KA

c) EB > AC.

d) Ba đường thẳng AC, BD, KE cùng đi qua một điểm (nếu học)

Bài 4) Cho tam giác nhọn ABC. Vẽ ra phía ngoài tam giác ABC các tam giác đều ABD và ACE. Gọi M là giao điểm của DC và BE. Chứng minh rằng:

a. ΔABE = ΔADC

b. = 120⁰

Bài 5) Cho ∆ABC vuông ở C, có = 60⁰, tia phân giác của góc BAC cắt BC ở E, kẻ EK vuông góc với AB. (K ∈ AB), kẻ BD vuông góc AE (D ∈AE).

Chứng minh a) AK=KB                 b) AD=BC

Bài 6) Cho ∆ABC cân tại A và hai đường trung tuyến BM, CN cắt nhau tại K

a) Chứng minh ∆BNC= ∆CMB

b) Chứng minh ∆BKC cân tại K

c) Chứng minh BC < 4.KM

Bài 7): Cho ∆ ABC vuông tại A có BD là phân giác, kẻ DE ⊥ BC ( E ∈ BC ). Gọi F là giao điểm của AB và DE.

Chứng minh rằng:

a) BD là trung trực của AE

b) DF = DC

c) AD < DC;

d) AE // FC.

Bài 8. Cho tam giác ABC vuông tại A, góc B có số đo bằng . Vẽ AH vuông góc với BC, (H ∈ BC).

a. So sánh AB và AC; BH và HC;

b. Lấy điểm D thuộc tia đối của tia HA sao cho HD = HA. Chứng minh rằng hai tam giác AHC và DHC bằng nhau.

c. Tính số đo của góc BDC.

Bài 9. Cho tam giác ABC cân tại A, vẽ trung tuyến AM. Từ M kẻ ME vuông góc với AB tại E, kẻ MF vuông góc với AC tại F.

a. Chứng minh ∆BEM = ∆CFM.

b. Chứng minh AM là trung trực của EF.

c. Từ B kẻ đường thẳng vuông góc với AB tại B, từ C kẻ đường thẳng vuông góc với AC tại C, hai đường thẳng này cắt nhau tại D. Chứng minh rằng ba điểm A, M, D thẳng hàng.

Bài 10)

Cho tam giác ABC cân tại A, đường cao AH. Biết AB = 5 cm, BC = 6 cm.

a) Tính độ dài các đoạn thẳng BH, AH?

b) Gọi G là trọng tâm tam giác ABC. Chứng minh rằng ba điểm A, G, H thẳng hàng.

c) Chứng minh hai góc ABG và ACG bằng nhau

Bài 11. Cho ∆ABC (Â = ); BD là phân giác của góc B (D∈AC). Trên tia BC lấy điểm E sao cho BA = BE. a) Chứng minh DE ⊥ BE. b) Chứng minh BD là đường trung trực của AE. c) Kẻ AH ⊥ BC. So sánh EH và EC.

Bài 12): Cho tam giác nhọn ABC có AB > AC, vẽ đường cao AH. a. Chứng minh HB > HC b. So sánh góc BAH và góc CAH. c. Vẽ M, N sao cho AB, AC lần lượt là trung trực của các đoạn thẳng HM, HN. Chứng minh tam giác MAN là tam giác cân.

Bài 13): Cho tam giác nhọn ABC có AB > AC, vẽ đường cao AH.

a. Chứng minh HB > HC

b. So sánh góc BAH và góc CAH.

c. Vẽ M, N sao cho AB, AC lần lượt là trung trực của các đoạn thẳng HM, HN.

Chứng minh tam giác MAN là tam giác cân.

Bai 14) Cho góc nhọn xOy, trên 2 cạnh Ox, Oy lần lượt lấy 2 điểm A và B sao cho OA = OB, tia phân giác của góc xOy cắt AB tại I.

a) Chứng minh OI ⊥ AB .

b) Gọi D là hình chiếu của điểm A trên Oy, C là giao điểm của AD với OI. Chứng minh BC ⊥ Ox .p

Bài 15) Cho tam giác ABC có góc A = 90^o , AB = 8cm, AC = 6cm .

a. Tính BC .

b. Trên cạnh AC lấy điểm E sao cho AE= 2cm; trên tia đối của tia AB lấy điểm D sao cho AD=AB. Chứng minh ∆BEC = ∆DEC .

c. Chứng minh DE đi qua trung điểm cạnh BC .

III. Một số đề tham khảo thi học kì 2 Toán 7

Đề thi thử học kì 2 Toán 7 số 1

Bài 1: Thời gian giải 1 bài toán của 40 học sinh được ghi trong bảng sau: (Tính bằng phút)

8	10	10	8	8	9	8	9
8	9	9	12	12	10	11	8
8	10	10	11	10	8	8	9
8	10	10	8	11	8	12	8
9	8	9	11	8	12	8	9

a) Dấu hiệu ở đây là gì? Số các dấu hiệu là bao nhiêu?

b) Lập bảng tần số.

c) Nhận xét

d)Tính số trung bình cộng , Mốt

e) Vẽ biểu đồ đoạn thẳng.

Bài 2 : Cho : P(x) = - 2x² + 3x⁴ + x³ +x² - x

Q(x) = -6x⁴ + 3x² - 2 - 4x³ – 2x²

a. Sắp xếp các hạng tử của mỗi đa thức theo luỹ thừa giảm dần của biến.

b. Tính P(x) + Q(x) và P(x) - Q(x)

c. Chứng tỏ x = 0 là nghiệm của đa thức P(x), nhưng không phải là nghiệm của đa thức Q(x)

Bài 3 : Cho đa thức : P(x) = x⁴ + 3x² + 3

a)Tính P(1), P(-1).

b)Chứng tỏ rằng đa thức trên không có nghiệm.

Bài 4 : Cho ABC vuông tại A, có AB < AC. Trên cạnh BC lấy điểm D sao cho BD = BA. Kẻ AH

vuông góc với BC, kẻ DK vuông góc với AC.

a)Chứng minh : =

b)Chứng minh: AD là phân giác của góc HAC

c) Chứng minh : AK = AH.

d) Chứng minh : AB + AC < BC +AH

Đề thi thử học kì 2 Toán 7 số 2

Bài 1 : Thế nào là 2 đơn thức đồng dạng? Cho 4 đơn thức đồng dạng với đơn thức -4x⁵y³

Bài 2 : Thu gọn các đa thức sau rồi tìm bậc của chúng:

a) 5x²yz(-8xy³z);

b) 15xy²z(-4/3x²yz³). 2xy

Bài 3 : Cho 2 đa thức : A = -7x²- 3y² + 9xy -2x² + y²

B = 5x² + xy – x² – 2y²

a)Thu gọn 2 đa thức trên.

b) Tính C = A + B ;

c) Tính C khi x = -1 và y = -1/2

Bài 4 :Tìm hệ số a của đa thức A(x) = ax² +5x – 3, biết rằng đa thức có 1 nghiệm bằng 1/2 ?

Bài 5: Cho tam giác cân ABC có AB = AC = 5 cm , BC = 8 cm . Kẻ AH vuông góc với BC (H € BC)

a) Chứng minh : HB = HC và =

b)Tính độ dài AH ?

c)Kẻ HD vuông góc AB ( D€AB), kẻ HE vuông góc với AC(E€AC). Chứng minh : DE//BC

Đề thi thử học kì 2 Toán 7 số 3

Bài 1: Tìm hiểu thời gian làm 1 bài tập (thời gian tính theo phút) của 35 học sinh (ai cũng làm được) thì người ta lập được bảng sau:

Thời gian	3	4	5	6	7	8	9	10	11	12
Số học sinh	1	3	5	9	6	4	3	2	1	1	N= 35

a) Dấu hiệu ở đây là gì? Tìm mốt của dấu hiệu.

b) Tính số trung bình cộng

c) Vẽ biểu đồ đoạn thẳng

Bài 2: Thu gọn các đơn thức sau, rồi tìm bậc của chúng :

a) 2x²(-3xy³z) ;

b) (-12xyz).( -4/3x²yz³)y

Bài 3: Cho P(x) = 1 + 2x⁵ -3x² + x⁵ + 3x³ – x⁴ – 2x

Q(x) = -3x⁵ + x⁴ -2x³ +5x -3 –x +4 +x²

a)Thu gọn và sắp xếp các hạng tử của mỗi đa thức theo luỹ thừa giảm của biến.

b)Tính P(x) + Q(x)

c)Gọi N là tổng của 2 đa thức trên. Tính giá trị của đa thức N tại x =1

Bài 4: Cho tam giác DEF vuông tại D, phân giác EB. Kẻ BI vuông góc với EF tại I. Gọi H là giao điểm của ED và IB. Chứng minh:

a)Tam giác EDB = Tam giác EIB

b)HB = BF

c)DB < BF

d)Gọi K là trung điểm của HF. Chứng minh 3 điểm E, B, K thẳng hàng

Đề thi thử học kì 2 Toán 7 số 4

Bài 1. Điểm kiểm tra toán của 1 lớp 7 được ghi như sau:

a) Lập bảng tần số. Tính số trung bình cộng, tìm Mốt của dấu hiệu

b) Vẽ biểu đồ đoạn thẳng

Bài 2: Cho 2 đa thức:

M(x) = 3x³ + x² + 4x⁴ – x – 3x³ + 5x⁴ + x² – 6

N(x) = - x² – x⁴ + 4x³ – x² -5x³ + 3x + 1 + x

a. Thu gọn và sắp xếp các đa thức trên theo luỹ thừa giảm dần của biến

b. Tính: M(x) + N(x) ; M(x) – N(x)

c. Đặt P(x) = M(x) – N(x). Tính P(x) tại x = -2

Bài 3: Tìm m, biết rằng đa thức Q(x) = mx² + 2mx – 3 có 1 nghiệm x = -1

Bài 4: Cho tam giác ABC vuông tại A. Đường phân giác của góc B cắt AC tại H. Kẻ HE vuông góc với BC ( E € BC). Đường thẳng EH và BA cắt nhau tại I.

a/ Chứng minh rẳng: ΔABH = ΔEBH;

b/ Chứng minh BH là trung trực của AE

c/ So sánh HA và HC;

d/ Chứng minh BH vuông góc với IC. Có nhận xét gì về tam giác IBC

Đề thi thử học kì 2 Toán 7 số 5

Bài 1: Số lượng học sinh của từng lớp trong một trường THCS được ghi trong bảng như sau:

40	37	38	40	39	40	35	36	39	40
36	40	36	40	40	35	39	36	36	39
40	39	39	36	39	39	40	37	39	40
38	40	40	40	37	39	40	36	37	40

b/ Có bao nhiêu giá trị khác nhau của dấu hiệu?

c/ Lập bảng tần số?

d/Tính số trung bình cộng và tìm mốt của dấu hiệu?

e/Vẽ biểu đồ đoạn thẳng?

Bài 2: Cho : P(x) = - 3x² + 3x⁴ + 5x³ +x² - x – 2

Q(x) = -2x⁴ + x² - 9 - 3x³ – x²

a/ Sắp xếp các hạng tử của mỗi đa thức theo luỹ thừa giảm dần của biến.

b/ Tính P(x) + Q(x) và P(x) - Q(x)

c/ Tính : 2 P(x) + 5 Q(x) và 4 P(x) – 3 Q(x)

Bài 3: Cho tam giác nhọn ABC. Vẽ ra phía ngoài tam giác ABC các tam giác đều ABD và ACE. Gọi M là giao điểm của DC và BE. Chứng minh rằng:

a)

b) BMC = 120⁰

Bài 4: Cho tam giác ABC cân tại A, Â = 100⁰.D là một điểm thuộc miền trong của tam giác ABC sao cho góc DBC =10⁰, DCB = 20⁰. Tính góc ABD.

Còn tiếp........

Trước mỗi kỳ thi quan trọng, các em học sinh không thể bỏ qua đề cương ôn thi cho từng môn. Đây là những tài liệu hữu ích giúp các em có kế hoạch ôn thi rõ ràng, đi đúng trọng tâm kiến thức được học. Với những bộ đề cương ôn thi học kì 2 lớp 7 được giới thiệu trên Tìm Đáp Án, các em học sinh không chỉ tiết kiệm được thời gian xây dựng đề cương, mà thông qua đó còn giúp các em ôn tập và củng cố kiến thức đã học trong học kì 2 hiệu quả. Các em tham khảo các đề thi mới nhất sau đây để chuẩn bị cho kì thi sắp tới.

IV. Đề thi học kì 2 lớp 7 được tải nhiều nhất

• Đề kiểm tra học kì 2 lớp 7 môn Toán
• Bộ 25 đề thi học kì 2 môn Toán lớp 7
• Bộ đề thi học kì 2 môn Ngữ văn lớp 7 có đáp án
• Bộ đề thi học kỳ 2 môn Tiếng Anh lớp 7 CÓ ĐÁP ÁN
• Bộ đề thi học kì 2 môn Sinh học lớp 7
• Bộ đề thi học kì 2 môn Lịch sử lớp 7 có đáp án
• Bộ đề thi học kì 2 môn Địa lý lớp 7 có đáp án
• 10 đề thi học kì 2 lớp 7 môn Toán năm học 2020 - 2021

Trên đây, TimDapAnđã giới thiệu tới các bạn Đề cương ôn tập học kì 2 môn Toán lớp 7, hy vọng tài liệu sẽ giúp các em học sinh nắm vững phần lý thuyết trọng tâm của chương trình Toán lớp 7 học kì 2, từ đó biết cách vận dụng để giải các bài Toán liên quan. Ngoài ra, mời các bạn tham khảo thêm: Giải bài tập Toán lớp 7, Giải Vở BT Toán 7, Đề thi học kì 1 lớp 7, Đề thi giữa kì 1 lớp 7, Đề thi học kì 2 lớp 7... được cập nhật liên tục trên Tìm Đáp Án.

Ngoài việc ôn tập theo đề cương thì việc thực hành giải các đề thi học kì lớp 7 môn Toán cũng là việc rất thiết để các em học sinh làm quen với cấu trúc đề thi, giúp các em chủ động, tự tin hơn khi bước vào kì thi chính thức của mình. Các nội dung kiểm tra trong đề thi Toán lớp 7 học kì 2 đều là các kiến thức trọng tâm bám sát vào chương trình sách giáo khoa Toán 7, được tổng hợp cả bài tập cơ bản và nâng cao, thích hợp dành cho tất cả các em học sinh lớp 7 thực hành luyện tập. Sau đây là một số đề thi học kì 2 Toán 7 mới nhất năm 2021 trên Tìm Đáp Án, mời các bạn click vào các link sau để luyện đề nhé:

• Đề thi học kì 2 Toán 7 năm 2021 trường THCS Thăng Long, Hà Nội
• Đề thi học kì 2 Toán 7 năm 2021 trường chuyên Hà Nội Amsterdam
• Đề thi học kì 2 Toán 7 năm 2021 Phòng GD&ĐT Hiệp Hòa, Bắc Giang
• Đề thi học kì 2 lớp 7 môn Toán trường THCS Archimedes
• Đề thi học kì 2 Toán 7 năm 2021 trường THCS Cầu Giấy, Hà Nội
• Đề thi Toán lớp 7 học kì 2 năm 2021 có đáp án
• Đề thi học kì 2 Toán 7 năm 2021 có đáp án
• Đề thi học kì 2 Toán 7 năm 2021 trường Nguyễn Tất Thành, Hà Nội
• Đề thi HK2 Toán 7 trường THCS Hoàng Hoa Thám, Hà Nội năm 2020 - 2021