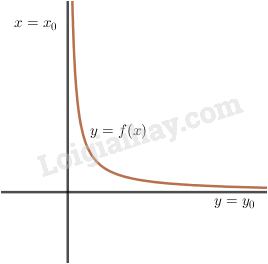
Lý thuyết đường tiệm cận

Cho hàm số \(y = f(x)\) có đồ thị \((C)\).

1. Tiệm cận đứng

Đường thẳng \(x=a\) là đường tiệm cận đứng của \((C)\) nếu một trong bốn điều kiện sau được thoả mãn:

\(\eqalign{
& \mathop {\lim }\limits_{x \to {a^ + }} f(x) = + \infty \cr
& \mathop {\lim }\limits_{x \to {a^ + }} f(x) = - \infty \cr
& \mathop {\lim }\limits_{x \to {a^ - }} f(x) = + \infty \cr
& \mathop {\lim }\limits_{x \to {a^ - }} f(x) = - \infty \cr} \)

2. Tiệm cận ngang

Đường thẳng \(y = b\) là tiệm cận ngang của \((C)\) nếu:

\(\eqalign{
& \mathop {\lim }\limits_{x \to + \infty } f(x) = b \cr
& \mathop {\lim }\limits_{x \to - \infty } f(x) = b \cr} \)

3. Chú ý

- Đồ thị hàm đa thức không có tiệm cận đứng và tiệm cận ngang, do đó trong các bài toán khảo sát và vẽ đồ thị hàm đa thức, ta không cần tìm các tiệm cận này.