Giải mục 1 trang 98, 99 SGK Toán 9 tập 1 - Chân trời sáng tạo
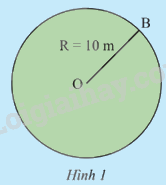
Một hàng rào bao quanh một sân cỏ hình tròn có bán kính 10 m (Hình 1) được ghép bởi 360 phần bằng nhau. Hãy tính: a) Độ dài của toàn bộ hàng rào b) Độ dài của mỗi phần hàng rào c) Độ dài của n phần hàng rào.
HĐ1
Trả lời câu hỏi Hoạt động 1 trang 98 SGK Toán 9 Chân trời sáng tạo
Một hàng rào bao quanh một sân cỏ hình tròn có bán kính 10 m (Hình 1) được ghép bởi 360 phần bằng nhau. Hãy tính:
a) Độ dài của toàn bộ hàng rào
b) Độ dài của mỗi phần hàng rào
c) Độ dài của n phần hàng rào.
Phương pháp giải:
Dựa vào công thức chu vi hình tròn: C = 2\(\pi \)R .
Lời giải chi tiết:
a) Ta có độ dài của toàn bộ hàng rào là:
C = 2\(\pi \)R = 2.\(\pi \).10 = 20\(\pi \) m
b) Độ dài của mỗi phần hàng rào là:
\(\frac{C}{{360}} = \frac{{20\pi }}{{360}} = \frac{\pi }{{18}}\) m
c) Độ dài của n phần hàng rào là: n.\(\frac{\pi }{{18}}\) m.
TH1
Trả lời câu hỏi Thực hành 1 trang 99 SGK Toán 9 Chân trời sáng tạo
Tính độ dài cung 72o của một đường tròn bán kính 25 cm.
Phương pháp giải:
Sử dụng công thức \(l = \frac{{\pi Rn}}{{180}}\).
Lời giải chi tiết:
Cung 72o , bán kính R = 25 cm có độ dài là:
\(l = \frac{{\pi Rn}}{{180}} = \frac{{\pi .25.72}}{{180}} \approx 31,42\)cm.
VD1
Trả lời câu hỏi Vận dụng 1 trang 99 SGK Toán 9 Chân trời sáng tạo
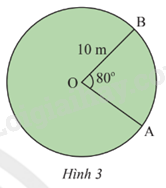
Tính độ dài của của đoạn hàng rào từ A đến B của sân cỏ trong Hình 3, cho biết \(\widehat {AOB} = {80^o}\).
Phương pháp giải:
- Dựa vào sđ\(\overset\frown{AB}\) = \(\widehat {AOB}\) (\(\overset\frown{AB}\) và góc \(\widehat {AOB}\) cùng chắn cung AB)
- Áp dụng công thức: \(l = \frac{{\pi Rn}}{{180}}\)
Lời giải chi tiết:
Ta có độ dài cung AB = \(\widehat {AOB} = {80^o}\), bán kính R = 10 m có độ dài là:
\(l = \frac{{\pi Rn}}{{180}} = \frac{{\pi .10.80}}{{180}} \approx 13,96\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải mục 1 trang 98, 99 SGK Toán 9 tập 1 - Chân trời sáng tạo timdapan.com"







