Bài 8 trang 103 SBT toán 9 tập 1

Đề bài

Cạnh huyền của một tam giác vuông lớn hơn một cạnh góc vuông là \(1cm\) và tổng của hai cạnh góc vuông lớn hơn cạnh huyền \(4cm\). Hãy tính các cạnh của tam giác vuông này. 

Lời giải chi tiết

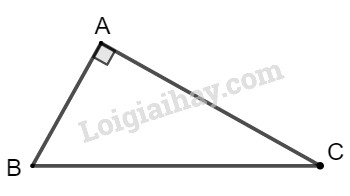
Giả sử tam giác ABC có \(\widehat {BAC} = 90^\circ \)

Theo đề  bài, ta có: \(BC - AB = 1(cm)\)  (1)

\(AB + AC - BC = 4(cm)\) (2)

Từ (1) và (2) suy ra:   

\((BC - AB) + (AB + AC - BC)\)\(=1+4\)
\(\Leftrightarrow  BC - AB + AB + AC - BC=5\)
\(\Leftrightarrow  AC=5\)

Theo định lý Pytago, ta có: \(B{C^2} = A{B^2} + A{C^2}\)    (3)

Từ (1) suy ra: \(BC = AB + 1\)   (4)

Thay (4) và (3) ta có:

\(\eqalign{
& {\left( {AB + 1} \right)^2} = A{B^2} + A{C^2} \cr 
& \Leftrightarrow A{B^2} + 2AB + 1 = A{B^2} + {5^2} \cr 
& \Leftrightarrow 2AB = 24 \cr 
& \Leftrightarrow AB = 12\left( {cm} \right) \cr} \)

Thay \(AB = 12\) (cm) vào (1) ta có: \(BC = 12 + 1 = 13(cm)\)