Bài 7 trang 103 SBT toán 9 tập 1
Giải bài 7 trang 103 sách bài tập toán 9. Đường cao của một tam giác vuông chia cạnh huyền thành hai đường thẳng có độ dài là 3 và 4. Hãy tính các cạnh góc vuông của tam giác này.
Đề bài
Đường cao của một tam giác vuông chia cạnh huyền thành hai đường thẳng có độ dài là 3 và 4. Hãy tính các cạnh góc vuông của tam giác này.
Phương pháp giải - Xem chi tiết
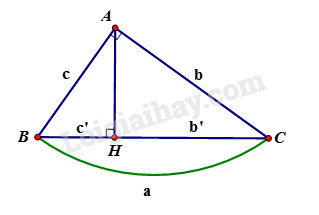
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\). Khi đó ta có các hệ thức sau:
+) \(A{B^2} = BH.BC\) hay \({c^2} = a.c'\)
+)\(A{C^2} = CH.BC\) hay \({b^2} = ab'\)
+) \(AB^2+AC^2=BC^2\) hay \(c^2+b^2=a^2\) (định lý Pytago)
Lời giải chi tiết

Giả sử tam giác ABC có: \(\widehat {BAC} = {90^0},\)\(AH \bot BC,BH = 3,CH = 4\)
Ta có \(BC=BH+CH=3+4=7\)
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
\(\eqalign{
& A{B^2} = BH.BC \cr
& = 3.7 = 21 \cr
& \Rightarrow AB = \sqrt {21}; \cr} \)
\(\eqalign{
& A{C^2} = CH.BC \cr
& = 4.7 = 28 \cr
& \Rightarrow AC = \sqrt {28} = 2\sqrt 7. \cr} \)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 7 trang 103 SBT toán 9 tập 1 timdapan.com"







