Bài 14 trang 104 SBT toán 9 tập 1
Giải bài 14 trang 104 sách bài tập toán 9. Cho hai đoạn thẳng có độ dài là a và b. Dựng đoạn thẳng căn ab....
Đề bài
Cho hai đoạn thẳng có độ dài là \(a\) và \(b\). Dựng đoạn thẳng \(\sqrt {ab} \) như thế nào?
Phương pháp giải - Xem chi tiết
Các bước để dựng hình theo giả thiết của bài toán:
Bước 1: Phân tích hình.
Bước 2: Dựng hình.
Bước 3: Chứng minh cách dựng trên thoả mãn yêu cầu của đề toán.
Bước 4 :Biện luận: Xem lại từng phép dựng đã thực hiện để xem có điều kiện ràng buộc không.Từ đó suy ra bài toán có mấy nghiệm hình.
Để chứng minh ta sử dụng:
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\).
Khi đó ta có hệ thức sau: \(AH^2=BH.CH\)
Lời giải chi tiết
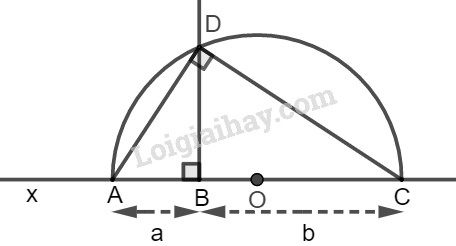
* Cách dựng:
− Dựng đường thẳng \(x\).
− Trên đường thẳng \(x\) dựng liên tiếp hai đoạn thẳng \(AB = a\), \(BC = b\).
− Dựng nửa đường tròn tâm \(O\) đường kính \(AC\).
− Từ \(B\) dựng đường thẳng vuông góc với \(AC\) cắt nửa đường tròn tâm \(O\) tại \(D\).
Ta có đoạn \(BD = \sqrt {ab} \) cần dựng.
* Chứng minh:
Nối \(DA\) và \(DC.\) Ta có tam giác \(ACD\) vuông tại \(D\) (do \(OD=OA=OC=\dfrac {AC}{2})\) và \(DB \bot AC\).
Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có:
\(B{D^2} = AB.BC = a.b\)
Suy ra: \(BD = \sqrt {ab} .\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 14 trang 104 SBT toán 9 tập 1 timdapan.com"







