Giải Bài 27 trang 75 sách bài tập toán 7 - Cánh diều
Cho bốn điểm A, B, C, D nằm trên đường tròn tâm O sao cho AB = CD. Chứng minh \(\widehat {AOB} = \widehat {COD}\)
Đề bài
Cho bốn điểm A, B, C, D nằm trên đường tròn tâm O sao cho AB = CD. Chứng minh \(\widehat {AOB} = \widehat {COD}\)
Phương pháp giải - Xem chi tiết
Xét các điều kiện các cạnh để chứng minh \(\Delta OAB = \Delta 0C{\rm{D}}(c - c - c)\) suy ra \(\widehat {AOB} = \widehat {CO{\rm{D}}}\)
Lời giải chi tiết
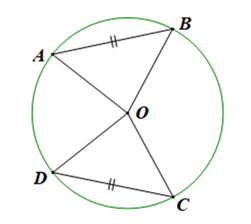
Vì bốn điểm A, B, C, D nằm trên đường tròn tâm O nên OA = OB = OC = OD.
Xét ∆OAB và ∆OCD có:
AO = OC (chứng minh trên),
AB = DC (giả thiết),
OB = OD (chứng minh trên),
Suy ra ∆OAB = ∆OCD (c.c.c).
Do đó \(\widehat {AOB} = \widehat {CO{\rm{D}}}\) (hai góc tương ứng).
Vậy \(\widehat {AOB} = \widehat {CO{\rm{D}}}\)
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải Bài 27 trang 75 sách bài tập toán 7 - Cánh diều timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải Bài 27 trang 75 sách bài tập toán 7 - Cánh diều timdapan.com"







