Bài 1.35 trang 32 SBT hình học 10

Cho tam giác \(ABC\) nội tiếp trong đường tròn tâm \(O\), \(H\) là trực tâm của tam giác, \(D\) là điểm đối xứng của \(A\) qua \(O\).

LG a

Chứng minh tứ giác \(HCDB\) là hình bình hành.

Phương pháp giải:

Chứng mình tứ giác có hai cặp cạnh đối diện song song.

Giải chi tiết:

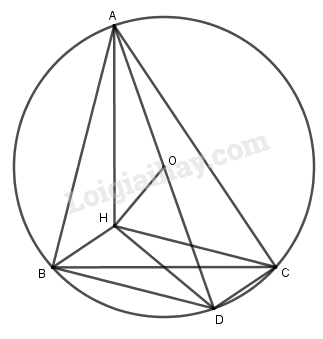
Vì \(AD\) là đường kính của đường tròn tâm \(O\) nên \(BD \bot AB,DC \bot AC\).

Ta có \(CH \bot AB,BH \bot AC\)nên suy ra \(CH // BD\) và \(BH // DC\).

Vậy tứ giác \(HCDB\) là hình bình hành.

LG b

Chứng minh: \(\overrightarrow {HA}  + \overrightarrow {HD}  = 2\overrightarrow {HO} \);

\(\overrightarrow {HA}  + \overrightarrow {HB}  + \overrightarrow {HC}  = 2\overrightarrow {HO} \);

\(\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC}  = \overrightarrow {OH} \).

Phương pháp giải:

Sử dụng tính chất của hình bình hành và tính chất trung điểm suy ra điều phải chứng minh.

Giải chi tiết:

 Vì \(O\) là trung điểm của \(AD\) nên \(\overrightarrow {HA}  + \overrightarrow {HD}  = 2\overrightarrow {HO} \) (1)

Vì tứ giác \(HCDB\) là hình bình hành nên ta có \(\overrightarrow {HB}  + \overrightarrow {HC}  = \overrightarrow {HD} \) (2)

Từ (1) và (2) suy ra: \(\overrightarrow {HA}  + \overrightarrow {HB}  + \overrightarrow {HC}  = 2\overrightarrow {HO} \) (3)

Theo quy tắc ba điểm, từ (3) suy ra \(\overrightarrow {HO}  + \overrightarrow {OA}  + \overrightarrow {HO}  + \overrightarrow {OB}  + \overrightarrow {HO}  + \overrightarrow {OC}  = 2\overrightarrow {HO} \)

Vậy \(\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC}  = \overrightarrow {OH} \) (4).

LG c

Gọi \(G\) là trọng tâm tam giác \(ABC\).

Chứng minh \(\overrightarrow {OH}  = 3\overrightarrow {OG} \)

Từ đó có kết luận gì về ba điểm \(O, H, G\)?

Phương pháp giải:

Sử dụng kết quả câu trên suy ra kết luận.

Giải chi tiết:

\(G \) là trọng tâm của tam giác \(ABC\).

Ta có \(\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC}  = 3\overrightarrow {OG} \).

Từ (4) suy ra \(\overrightarrow {OH}  = 3\overrightarrow {OG} \). Vậy ba điểm \(O, H, G\) thẳng hàng.

Nhận xét :

Trong một tam giác trực tâm \(H\), trọng tâm \(G\) và tâm đường tròn ngoại tiếp \(O\) thẳng hàng.