Bài 1.33 trang 32 SBT hình học 10
Giải bài 1.33 trang 32 sách bài tập hình học 10. Cho tứ giác ABCD...
Đề bài
Cho tứ giác \(ABCD\). Các điểm \(M, N , P\) và \(Q\) lần lượt là trung điểm của \(AB, BC, CD\) và \(DA\). Chứng minh rằng hai tam giác \(ANP\) và \(CMQ\) có cùng trọng tâm.
Phương pháp giải - Xem chi tiết
- Gọi \(G\) là trọng tâm của tam giác \(ANP\).
- Chứng minh \(\overrightarrow {GC} + \overrightarrow {GM} + \overrightarrow {GQ} = \overrightarrow 0 \) và kết luận.
Lời giải chi tiết
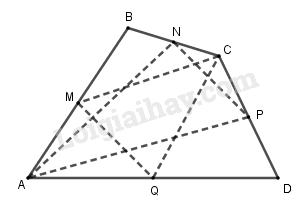
Gọi \(G \) là trọng tâm của tam giác \(ANP\).
Khi đó \(\overrightarrow {GA} + \overrightarrow {GN} + \overrightarrow {GP} = \overrightarrow 0 \)
Ta có: \(\overrightarrow {GC} + \overrightarrow {GM} + \overrightarrow {GQ} \)\( = \overrightarrow {GA} + \overrightarrow {AC} + \overrightarrow {GN} \) \( + \overrightarrow {NM} + \overrightarrow {GP} + \overrightarrow {PQ} \) \( = (\overrightarrow {GA} + \overrightarrow {GN} + \overrightarrow {GP} ) + \overrightarrow {AC} + (\overrightarrow {NM} + \overrightarrow {PQ} )\)
\( = \overrightarrow {AC} + \overrightarrow {CA} = \overrightarrow 0 \)
(Vì \(\overrightarrow {NM} = \dfrac{1}{2}\overrightarrow {CA} ,\overrightarrow {PQ} = \dfrac{1}{2}\overrightarrow {CA} \) nên \(\overrightarrow {NM} + \overrightarrow {PQ} = \overrightarrow {CA} \)).
Vậy \(\overrightarrow {GC} + \overrightarrow {GM} + \overrightarrow {GQ} = \overrightarrow 0 \)
Suy ra \(G\) là trọng tâm của tam giác \(CMQ\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 1.33 trang 32 SBT hình học 10 timdapan.com"







