Đề kiểm tra 45 phút (1 tiết) - Đề số 2 - Chương 2 - Đại số 9

Đề bài

Bài 1. Cho hai đường thẳng : \(y = 2x – 1\) (d₁) và \(y = -x + 2\) (d₂).

a. Tìm tọa độ giao điểm M của (d₁) và (d₂) .

b. Viết phương trình đường thẳng (d) qua M nói trên và cắt trục Oy tại điểm có tung độ bằng 4.

c. Viết phương trình đường thẳng (d’) qua gốc tọa độ O và song song với (d₁)

Bài 2. Cho đường thẳng (d): \(y = ax + b \;( a ≠ 0)\)

a. Tìm a, b biết rằng phương trình đường thẳng đi qua hai điểm \(A(1; 2)\) và \(B(2; 0)\).

b. Vẽ đồ thị của hàm số \(y = ax + b\) với a, b vừa tìm được ở câu a

Lời giải chi tiết

Bài 1. a. Phương trình hoành độ giao điểm của (d₁) và (d₂):

\(2x - 1 = -x + 2 ⇔ 3x = 3 ⇔ x = 1\)

Thế \(x = 1\) vào phương trình của (d₁) \(⇒ y = 2.1 – 1 ⇒ y = 1\).

Vậy \(M(1; 1)\).

b. Phương trình đường thẳng (d) có dạng: \(y = ax + b\; (a ≠ 0)\)

Đường thẳng (d) cắt Oy tại điểm có tung độ bằng \(4 ⇒ b = 4\)

Khi đó: \(y = ax + 4\).

\(M ∈ (d) ⇒ 1 = a.1 + 4 ⇒ a = -3\).

Vậy : \(y = -3x + 4\).

c. Vì (d’) // (d₁) nên (d’) có phương trình: \(y = 2x + b \;(b ≠ -1)\)

Vì \(O ∈ (d’) ⇒ b = 0\). Vậy phương trình của (d’) là : \(y = 2x\).

Bài 2. a. \(A ∈ (d)\) nên ta có:

\(2 = a + b ⇒ b = 2 – a\)  (1)

\(B ∈ (d)\) nên ta có:

\(0 = 2a + b ⇒ b = -2a\)  (2)

Từ (1) và (2) \(⇒ 2 – a = -2a ⇒ a = -2\)

Khi đó \(b = 4\).

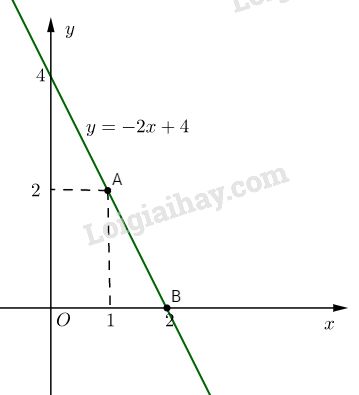
Vậy : \(y = -2x + 4\).

b. Đường thẳng \(y = -2x + 4\) qua \(A(1; 2)\) và \(B(2; 0)\).