Câu 4 trang 212 SGK Giải tích 12 Nâng cao
Hỏi nếu in 50000 tờ quảng cáo thì phải sử dụng bao nhiêu máy để được lãi nhiều nhất?
Đề bài
Một xưởng in có 8 máy in, mỗi máy in được 3600 bản in trong một giờ. Chi phí để vận hành một máy trong mỗi lần in là 50 nghìn đồng. Chi phí để n máy chạy trong một giờ là 10(6n + 10) nghìn đồng.
Hỏi nếu in 50000 tờ quảng cáo thì phải sử dụng bao nhiêu máy để được lãi nhiều nhất?
Phương pháp giải - Xem chi tiết
- Lập hàm số chi phí cần bỏ ra theo ẩn là số máy in sử dụng.
- Số lãi có được nhiều nhất khi chi phí bỏ ra là ít nhất nên cần đi tìm GTNN của hàm số trên.
Lời giải chi tiết
Gọi x là số máy in được sử dụng (x nguyên, 1 ≤ x ≤ 8)
Một giờ, mỗi máy in được 3600 bản nên x máy in được 3600x bản.
Khi đó, thời gian in 50000 tờ quảng cáo là:
\({{50000} \over {3600x}}\,(h) = {{125} \over {9x}}\,(h)\)
Tổng chi phí để in 50000 tờ quảng cáo là:
\(f(x) = {{125} \over {9x}}(6x + 10).10 + 50x\) (nghìn đồng)
Số lãi sẽ nhiều nhất nếu chi phí ít nhất
Ta cần tìm giá trị nhỏ nhất của f(x) trên [1, 8]
Ta có:
\(\eqalign{
& f(x) = {{2500} \over 3} + 50x + {{12500} \over {9x}};x \in {\rm{[}}1,\,8{\rm{]}} \cr
& f'(x) = 50 - {{12500} \over {9{x^2}}} = {{50(9{x^2} - 250)} \over {9{x^2}}} \cr
& f'(x) = 0 \Leftrightarrow x = \sqrt {{{250} \over 9}} \approx 5,3 \cr} \)
Bảng biến thiên:
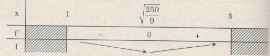
Trên [1, 8] đạt giá trị nhỏ nhất tại \(x = \sqrt {{{250} \over 9}} \)
Vì \(x\) nguyên nên khi sử dụng 5 máy thì thì thu được nhiều lãi nhất.
Chú ý:
Trong bài toán này, vì số máy in chỉ thuộc từ 1 đến 8 nên các em có thể thay trực tiếp x=1,2,...,8 và hàm số và tìm GTNN.
Search google: "từ khóa + timdapan.com" Ví dụ: "Câu 4 trang 212 SGK Giải tích 12 Nâng cao timdapan.com"







