Câu 16 trang 213 SGK Giải tích 12 Nâng cao

LG a

Cho hình thang cong A giới hạn bởi đồ thị hàm số y = e^x, trục hoành và các đường thẳng x = 0 và x = 1.

Tính thể tích của khối tròn xoay tạo được khi quay A quanh trục hoành.

Phương pháp giải:

Sử dụng công thức \(V = \int\limits_a^b {{f^2}\left( x \right)dx} \)

Lời giải chi tiết:

Thể tích cần tìm là:

\(\eqalign{
& V = \pi \int\limits_0^1 {{{({e^x})}^2}dx = \pi \int\limits_0^1 {{e^{2x}}dx} } \cr 
& = {\pi \over 2}{e^{2x}}|_0^1\,\, = {{\pi ({e^2} - 1)} \over 2} \cr} \) 

LG b

Cho hình phẳng B giới hạn bởi parabol y = x² + 1 và đường thẳng y = 2.

Tính thể tích khối tròn xoay tạo được khi quay B quanh trục tung.

Phương pháp giải:

Sử dụng công thức \(V = \int\limits_a^b {{f^2}\left( y \right)dy} \)

Lời giải chi tiết:

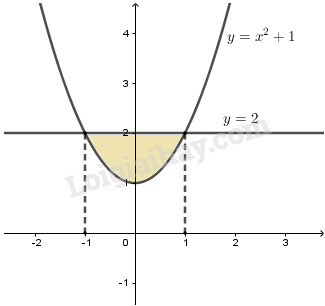
Ta có: \(y = {x^2} + 1 \Leftrightarrow {x^2} = y - 1 \) \(\Leftrightarrow x =  \pm \sqrt {y - 1} \)

x=0 thì y=1.

Thể tích cần tìm là:

\(\eqalign{
& V = \pi \int\limits_1^2 {{{(\sqrt {y - 1} )}^2}dy\,\,\, = } \pi \int\limits_1^2 {(y - 1)dy} \cr 
& = \pi ({{{y^2}} \over 2} - y)|_1^2\,\,\, = \,\,{\pi \over 2} \cr} \)