Bài 1.27 trang 15 SBT Giải tích 12 Nâng cao

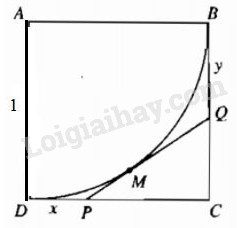
Cho hình vuông ABCD với cạnh có độ dài bằng 1 và cung BD là một phần tư đường tròn tâm A, bán kính AB chứa trong hình vuông (h.1.4). Tiếp tuyến tại M của cung BD cắt đoạn thẳng CD tại điểm P và cắt đoạn thẳng BC tại điểm Q. Đặt x = DP và y = BQ

LG a

Chứng minh rằng

\(P{Q^2} = {x^2} + {y^2} - 2x - 2y + 2\) và \(PQ = x + y\)

Từ đó tính y theo x

Lời giải chi tiết:

Tam giác PCQ vuông tại C có \(PC = 1 - x,QC = 1 - y\) và vuông tại C nên theo Pitago ta có:

\(\begin{array}{l}P{Q^2} = P{C^2} + C{Q^2}\\ = {\left( {1 - x} \right)^2} + {\left( {1 - y} \right)^2}\\ = 1 - 2x + {x^2} + 1 - 2y + {y^2}\\ = {x^2} + {y^2} - 2x - 2y + 2\end{array}\)

Lại có,

BC, QP là tiếp tuyến với đường tròn \(\left( {A;AB} \right)\) cắt nhau tại Q nên \(QM = QB = y\)

DC, QP là tiếp tuyến với đường tròn \(\left( {A;AB} \right)\) cắt nhau tại P nên \(PM = PD = y\)

Vậy \(PQ = PM + MQ = x + y\).

\(\begin{array}{l}
\Rightarrow P{Q^2} = {\left( {x + y} \right)^2} = {x^2} + 2xy + {y^2}\\
\Rightarrow {x^2} + {y^2} - 2x - 2y + 2 = {x^2} + 2xy + {y^2}\\
\Leftrightarrow 2xy + 2x + 2y - 2 = 0\\
\Leftrightarrow xy + x + y - 1 = 0\\
\Leftrightarrow y\left( {x + 1} \right) = 1 - x\\
\Leftrightarrow y = \frac{{1 - x}}{{x + 1}}
\end{array}\)

Vậy \(y = {{1 - x} \over {x + 1}},0 < x < 1\)

LG b

Tính PQ theo x và tìm x để PQ có độ dài nhỏ nhất.

Lời giải chi tiết:

\(\begin{array}{l}
PQ = x + y = x + \frac{{1 - x}}{{x + 1}}\\
= \frac{{{x^2} + x + 1 - x}}{{x + 1}} = \frac{{{x^2} + 1}}{{x + 1}}
\end{array}\)

Do đó, \(PQ = {{{x^2} + 1} \over {x + 1}},0 < x < 1\).

Xét hàm

\(\begin{array}{l}
f\left( x \right) = \frac{{{x^2} + 1}}{{x + 1}}\\
f'\left( x \right) = \frac{{2x\left( {x + 1} \right) - \left( {{x^2} + 1} \right)}}{{{{\left( {x + 1} \right)}^2}}}\\
= \frac{{{x^2} + 2x - 1}}{{{{\left( {x + 1} \right)}^2}}}\\
f'\left( x \right) = 0 \Leftrightarrow {x^2} + 2x - 1 = 0\\
\Leftrightarrow \left[ \begin{array}{l}
x = \sqrt 2 + 1 \notin \left( {0;1} \right)\\
x = \sqrt 2 - 1 \in \left( {0;1} \right)
\end{array} \right.
\end{array}\)

Do đó, đoạn thẳng PQ có độ dài nhỏ nhất khi \(x = \sqrt 2  - 1\)