Bài 9 trang 79 Tài liệu dạy – học Toán 9 tập 2
Giải bài tập Hai đường tròn (O; R) và (O’ ; R’) cắt nhau tại A và B. Cho biết số đo hai cung nhỏ
Đề bài
Hai đường tròn (O; R) và (O’ ; R’) cắt nhau tại A và B. Cho biết số đo hai cung nhỏ AB của hai đường tròn này bằng nhau. Chứng mình R = R’.
Phương pháp giải - Xem chi tiết
+) Chứng minh OO’ là trung trực của AB, từ đó chứng minh OO’ là phân giác của \(\widehat {AOB}\) và \(\widehat {AO'B}\).
+) Chứng minh tam giác AOO’ cân tại A.
Lời giải chi tiết
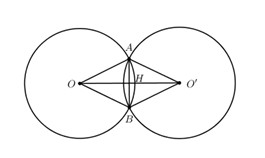
Ta có \(OA = OB = R \Rightarrow O\) thuộc trung trực của AB.
\(O'A = O'B = R' \Rightarrow O'\) thuộc trung trực của AB.
\( \Rightarrow OO'\) là trung trực của AB.
Gọi \(H = OO' \cap AB \Rightarrow OO' \bot AB\) tại H là H là trung điểm của AB.
Vì biết số đo hai cung nhỏ AB của hai đường tròn này bằng nhau nên \(\widehat {AOB} = \widehat {AO'B}\).
Tam giác OAB cân tại O \( \Rightarrow \) Đường cao OH đồng thời là đường phân giác \( \Rightarrow \widehat {AOH} = \dfrac{1}{2}\widehat {AOB}\).
Chứng minh hoàn toàn tương tự ta có \(\widehat {AO'H} = \dfrac{1}{2}\widehat {AO'B}\).
Mà \(\widehat {AOB} = \widehat {AO'B} \Rightarrow \widehat {AOH} = \widehat {AO'H} \) \(\Rightarrow \Delta AOO'\) cân tại A (Tam giác có 2 góc kề 1 cạnh bằng nhau) \( \Rightarrow OA = O'A \Rightarrow R = R'\) (đpcm).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 9 trang 79 Tài liệu dạy – học Toán 9 tập 2 timdapan.com"







