Bài 2 trang 79 Tài liệu dạy – học Toán 9 tập 2
Giải bài tập Cho tam giác đều ABC. Vẽ nửa đường tròn đường kính BC cắt AB và AC lần lượt tại D và E.
Đề bài
Cho tam giác đều ABC. Vẽ nửa đường tròn đường kính BC cắt AB và AC lần lượt tại D và E. Hãy so sánh các cung sau: BD, DE, EC
Phương pháp giải - Xem chi tiết
Chứng minh tam giác OBD và OCE đều. Từ đó chứng minh \(\widehat {BOD} = \widehat {DOE} = \widehat {COE}\).
Lời giải chi tiết
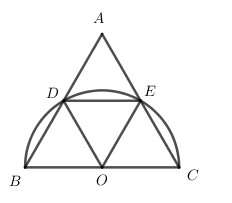
Gọi O là trung điểm của BC.
Xét tam giác BDO có: \(\left\{ \begin{array}{l}OB = OD = R\\\widehat {OBD} = {60^0}\,\,\left( {gt} \right)\end{array} \right. \Rightarrow \Delta BDO\) đều \( \Rightarrow \widehat {BOD} = {60^0}\).
Chứng minh hoàn toàn tương tự ta chứng minh được tam giác OCE đều \( \Rightarrow \widehat {COE} = {60^0}\)
Do B, O, C thẳng hàng
\(\begin{array}{l} \Rightarrow \widehat {BOD} + \widehat {DOE} + \widehat {COE} = {180^0}\\ \Rightarrow \widehat {DOE} = {180^0} - \widehat {BOD} - \widehat {COE}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {180^0} - {60^0} - {60^0} = {60^0}\\ \Rightarrow \widehat {BOD} = \widehat {DOE} = \widehat {COE}\end{array}\)
Nên cung BD = cung DE = cung EC.
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 2 trang 79 Tài liệu dạy – học Toán 9 tập 2 timdapan.com"







