Bài 5 trang 79 Tài liệu dạy – học Toán 9 tập 2
Giải bài tập Dây cung AB chia đường tròn tâm O thành hai cung. Cung lớn có số đo bằng ba lần cung nhỏ.
Đề bài
Dây cung AB chia đường tròn tâm O thành hai cung. Cung lớn có số đo bằng ba lần cung nhỏ.
a) Tính số đo mỗi cung.
b) Chứng minh khoảng cách OH từ tâm O đến dây cung AB có độ dài bằng \(\dfrac{{AB}}{2}\) .
Phương pháp giải - Xem chi tiết
a) Gọi số đo cung nhỏ AB là x, thì số đo cung lớn AB là \({360^0} - x\). Sử dụng giả thiết cung lớn có số đo bằng ba lần cung nhỏ tìm x.
b) Sử dụng định lí: Trong tam giác vuông trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy.
Lời giải chi tiết
a) Gọi số đo cung nhỏ AB là x, thì số đo cung lớn AB là \({360^0} - x\).
Vì cung lớn có số đo bằng ba lần cung nhỏ nên ta có \(360 - x = 3x \Leftrightarrow 4x = 360 \Leftrightarrow x = 90\).
Vậy số đo cung nhỏ AB bằng 900, số đo cung lớn AB bằng 2700.
b)
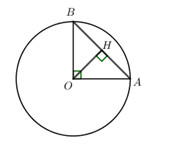
Kẻ \(OH \bot AB \Rightarrow H\) là trung điểm của AB (Quan hệ vuông góc giữa đường kính và dây cung)
\( \Rightarrow OH\) là đường trung tuyến của tam giác vuông ABC.
\( \Rightarrow OH = \dfrac{{AB}}{2}\) (Trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 5 trang 79 Tài liệu dạy – học Toán 9 tập 2 timdapan.com"







