Bài 14 trang 80 Tài liệu dạy – học Toán 9 tập 2
Giải bài tập Cho đường tròn tâm O đường kính AB. Trên nửa đường tròn lấy hai điểm C, D. Vẽ dây cung CE
Đề bài
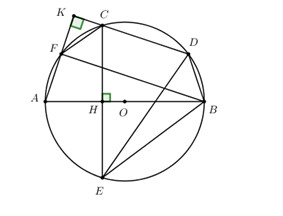
Cho đường tròn tâm O đường kính AB. Trên nửa đường tròn lấy hai điểm C, D. Vẽ dây cung CE vuông góc với AB tại H,vẽ AK vuông góc với CD tại K và cắt đường tròn tại F.
Chứng minh DE = BF
Phương pháp giải - Xem chi tiết
+) Chứng minh CD // BF
+) Chứng minh \(BC = BE \Rightarrow cung\,BC = cung\,BE\), từ đó suy ra \( \Rightarrow cung\,CF = cung\,BD \Rightarrow cung\,DF = cung\,BC\) .
Lời giải chi tiết
Xét tam giác ABF có \(OF = \dfrac{1}{2}AB = R \Rightarrow \Delta ABF\)vuông tại F \( \Rightarrow AF \bot BF\)
Mà \(AF \bot CD\,\,\left( {gt} \right) \Rightarrow BF//CD \)
\(\Rightarrow cung\,CF = cung\,BC\,\,\,\left( 1 \right)\).
=> cung DF = cung BC
Ta có \(AB \bot CE\) tại H \( \Rightarrow H\) là trung điểm của CE (Quan hệ vuông góc giữa đường kính và dây cung) \( \Rightarrow AB\) là trung trực của CE \( \Rightarrow BC = BE \)
\(\Rightarrow cung\,BC = cung\,BE\,\,\left( 2 \right)\) (Hai dây bằng nhau căng hai cung bằng nhau)
Từ (1) và (2) \( \Rightarrow cung\,BE = cung\,DF \)
\(\Rightarrow cung\,DE = cung\,BF\) \( \Rightarrow DE = BF\) (Hai cung bằng nhau căng hai dây bằng nhau) (đpcm).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 14 trang 80 Tài liệu dạy – học Toán 9 tập 2 timdapan.com"







