Bài 1 trang 79 Tài liệu dạy – học Toán 9 tập 2
Giải bài tập Cho đường tròn (O; 5 cm) và điểm M với OM = 10 cm. Qua M vẽ hai tiếp tuyến của đường tròn (O) tại A và B. Tính các góc ở tâm xác định bởi hai tia OA và OB.
Đề bài
Cho đường tròn (O; 5 cm) và điểm M với OM = 10 cm. Qua M vẽ hai tiếp tuyến của đường tròn (O) tại A và B. Tính các góc ở tâm xác định bởi hai tia OA và OB.
Phương pháp giải - Xem chi tiết
Gọi C là trung điểm của OM, chứng minh tam giác OAC đều.
Sử dụng tính chất hai tiếp tuyến cắt nhau: Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm.
Lời giải chi tiết
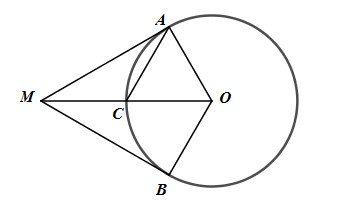
Gọi C là trung điểm của OM \( \Rightarrow OC = \dfrac{1}{2}OM = 5 \Rightarrow C\) thuộc đường tròn \(\left( {O;5cm} \right)\).
Tam giác OAM vuông tại A có AC là đường trung tuyến
\( \Rightarrow AC = \dfrac{1}{2}OM = OC = OA = 5cm\)
\(\Rightarrow \Delta OAC\) đều \( \Rightarrow \widehat {AOC} = {60^0}\)
Lại có OM là đường phân giác của \(\widehat {AOB}\) (tính chất 2 tiếp tuyến cắt nhau)
\( \Rightarrow \widehat {AOB} = 2\widehat {AOC} = {2.60^0} = {120^0}\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 1 trang 79 Tài liệu dạy – học Toán 9 tập 2 timdapan.com"







