Bài 12 trang 79 Tài liệu dạy – học Toán 9 tập 2
Giải bài tập a) Chứng minh rằng đường kính đi qua điểm chính giữa của một cung thì đi qua trung điểm của
Đề bài
a) Chứng minh rằng đường kính đi qua điểm chính giữa của một cung thì đi qua trung điểm của dây căng cung ấy. Mệnh đề đảo có đúng không ? Em hãy nêu thêm điều kiện để mệnh đề đảo đúng.
b) Chứng minh rằng đường kính đi qua điểm chính giữa của một cung thì vuông góc với dây căng cung ấy và ngược lại.
Phương pháp giải - Xem chi tiết
Chứng minh các tam giác bằng nhau.
Lời giải chi tiết
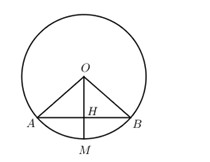
a) Gọi M là điểm chính giữa của cung AB ta có \(cung\,AM = cung\,BM \) \(\Rightarrow \widehat {AOM} = \widehat {BOM}\).
Gọi \(H = AB \cap OM\).
Xét tam giác AOH và tam giác BOH có:
\(OA = OB = R\);
\(\widehat {AOM} = \widehat {BOM}\,\,\left( {cmt} \right);\)
OH chung.
\( \Rightarrow \Delta AOH = \Delta BOH\,\,\left( {c.g.c} \right) \) \(\Rightarrow AH = BH \)
\(\Rightarrow H\) là trung điểm của AB.
Vậy đường kính đi qua điểm chính giữa của một cung thì đi qua trung điểm của dây căng cung ấy.
Mệnh đề đảo: Đường kính đi quan trung điểm của một dây cung thì đi qua điểm chính giữa của cung căng dây ấy.
Gọi H là trung điểm của AB ta có \(AH = BH\). Kéo dài OH cắt đường tròn tâm O tại M.
Xét tam giác AOH và tam giác BOH có:
\(\begin{array}{l}OA = OB = R;\\OH\,\,chung;\\AH = BH\,\,\left( {gt} \right);\\ \Rightarrow \Delta AOH = \Delta BOH\,\,\left( {c.c.c} \right) \\\Rightarrow \widehat {AOH} = \widehat {BOH}\end{array}\)
Hay \(\widehat {AOM} = \widehat {BOM} \)
\(\Rightarrow cung\,AM = cung\,BM \)
\(\Rightarrow M\) là điểm chính giữa của cung AB.
Vậy mệnh đề đảo đúng.
b) Theo ý a) ta chứng minh được \(\Delta AOH = \Delta BOH \Rightarrow \widehat {OHA} = \widehat {OHB}\).
Mà \(\widehat {OHA} + \widehat {OHB} = {180^0}\) (hai góc kề bù) \( \Rightarrow \widehat {OHA} = \widehat {OHB} = {90^0} \Rightarrow OM \bot AB\) tại H.
Vậy đường kính đi qua điểm chính giữa của một cung thì vuông góc với dây căng cung ấy.
Ngược lại: Ta cần chứng minh đường kính vuông góc với 1 dây thì đi qua điểm chính giữa của cung căng dây ấy.
Ta có \(OM \bot AB\) tại H.
Xét tam giác vuông OAH và tam giác vuông OBH có :
\(\begin{array}{l}OA = OB = R\\OH\,\,chung\end{array}\)
\( \Rightarrow {\Delta }OAH = {\Delta }OBH\) (cạnh huyền – cạnh góc vuông) \( \Rightarrow \widehat {AOM} = \widehat {BOM} \)
\(\Rightarrow cung\,AM = cung\,BM \)
\(\Rightarrow M\) là điểm chính giữa của cung AB.
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 12 trang 79 Tài liệu dạy – học Toán 9 tập 2 timdapan.com"







