Bài 20 trang 80 Tài liệu dạy – học Toán 9 tập 2
Giải bài tập Cho đường tròn O, đường kính AB. Qua trung điểm I của OA vẽ dây CD của (O) vuông góc với AB.
Đề bài
Cho đường tròn O, đường kính AB. Qua trung điểm I của OA vẽ dây CD của (O) vuông góc với AB.
a) Chứng minh ACOD là hình thoi.
b) Chứng minh tam giác BCD đều.
c) Vẽ dây CE // AB. Chứng minh D, O, E thẳng hàng.
d) Chứng minh ACEB là hình thang cân.
Phương pháp giải - Xem chi tiết
a) Chứng minh tứ giác ACOD có 4 cạnh bằng nhau.
b) Chứng minh \(\widehat {COD} = \widehat {DOB} = \widehat {COB}\), từ đó suy ra \(sd\,cung\,CD = sd\,cung\,DB = sd\,cung\,BC\), chứng tỏ tam giác BCD là tam giác có 3 cạnh bằng nhau.
c) Chứng minh tam giác OCE là tam giác đều, từ đo suy ra \(\widehat {COE} = {60^0}\). Chứng minh \(\widehat {DOE} = {180^0}\).
d) Chứng minh tức giác OCEB là hình thoi, từ đó suy ra OC // BE.
Tính góc EBA, chứng minh \(\widehat {EBA} = \widehat {CAO} = {60^0} \Rightarrow \) ACEB là hình thang cân.
Lời giải chi tiết
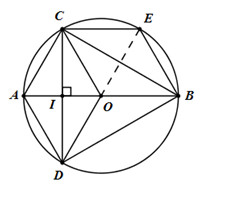
a) Ta có CD vuông góc với OA tại trung điểm I của OA
\( \Rightarrow CD\) là trung trực của OA \( \Rightarrow CA = CO;\,\,DA = DO\) (điểm thuộc trung trực của 1 đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó).
Mà \(CO = DO = R \) \(\Rightarrow CA = CO = DA = DO \)
\(\Rightarrow \) tứ giác ACOD là hình thoi (Tứ giác có 4 cạnh bằng nhau).
b) Xét tam giác OAC có \(CA = CO\,\,\left( {cmt} \right)\). Mà \(CO = OA = R \Rightarrow CA = CO = OA \) \(\Rightarrow \Delta OAC\) đều
\( \Rightarrow \widehat {AOC} = {60^0}\).
Vì ACOD là hình thoi nên OA là tia phân giác của góc COD \( \Rightarrow \left\{ \begin{array}{l}\widehat {COD} = 2\widehat {AOC} = {120^0}\\\widehat {AOD} = \widehat {AOC} = {60^0}\end{array} \right.\)
Ta có: \(\widehat {AOC} + \widehat {COB} = {180^0}\) (hai góc kề bù) \( \Rightarrow \widehat {COB} = {180^0} - \widehat {AOC} = {180^0} - {60^0} = {120^0}\).
Tương tự: \(\widehat {AOD} + \widehat {DOB} = {180^0}\) (hai góc kề bù) \( \Rightarrow \widehat {DOB} = {180^0} - \widehat {AOD} = {180^0} - {60^0} = {120^0}\).
\( \Rightarrow \widehat {COD} = \widehat {DOB} = \widehat {COB} = {120^0}\) \( \Rightarrow sd\,cung\,CD = sd\,cung\,DB = sd\,cung\,BC\) \( \Rightarrow CD = DB = BC\) (hai cung có số đo bằng nhau thì bằng nhau).
Do đó tam giác BCD là tam giác đều.
c) Vì CE // AB. Mà \(AB \bot CD \Rightarrow CE \bot CD\) tại C \( \Rightarrow \widehat {DCE} = {90^0}\).
Vì ACOD là hình thoi (cmt) nên tia CD là tia phân giác của góc ACO.
Mà tam giác OAC đều (cmt) \( \Rightarrow \widehat {ACO} = {60^0}\)\( \Rightarrow \widehat {DCO} = \dfrac{1}{2}\widehat {ACO} = \dfrac{1}{2}{.60^0} = {30^0}\)
Ta có \(\widehat {DCO} + \widehat {OCE} = \widehat {DCE}\)
\(\Leftrightarrow \widehat {OCE} = \widehat {DCE} - \widehat {DCO} = {90^0} - {30^0} = {60^0}\)
Xét tam giác OCE có \(\left\{ \begin{array}{l}OC = OE = R\\\widehat {OCE} = {60^0}\,\,\left( {cmt} \right)\end{array} \right. \Rightarrow \Delta OCE\) là tam giác đều \( \Rightarrow \widehat {COE} = {60^0}\)
\( \Rightarrow \widehat {DOE} = \widehat {COD} + \widehat {COE} = {120^0} + {60^0} = {180^0} \)
\(\Rightarrow D;O;E\) thẳng hàng.
d) Tam giác BCD đều có : \(\dfrac{{OB}}{{OI}} = \dfrac{{OB}}{{OB + OI}} = \dfrac{{OA}}{{OA + OI}} = \dfrac{{2OI}}{{2OI + OI}} = \dfrac{2}{3} \)
\(\Rightarrow O\) là trọng tâm tam giác đều BCD.
\( \Rightarrow DO\) là đường trung trực của BC.
Mà \(E \in DO \Rightarrow EB = EC\).
Lại có \(OB = OC = R;\,\,EC = OC\) (\(\Delta OCE\) đều) \( \Rightarrow OB = OC = EB = EC \Rightarrow \) Tứ giác OCEB là hình thoi (Tứ giác có 4 cạnh bằng nhau).
\( \Rightarrow OC//BE \Rightarrow \widehat {EBA} = \widehat {AOC}\) (hai góc đồng vị bằng nhau).
Mà \(\widehat {AOC} = {60^0}\,\,\left( {cmt} \right) \Rightarrow \widehat {EBA} = {60^0}\).
Xét tứ giác ACEB có AE // BC nên ACEB là hình thang. Lại có \(\widehat {CAO} = \widehat {EBA} = {60^0} \Rightarrow ACEB\) là hình thang cân (Hình thang có 2 góc ở đáy bằng nhau).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 20 trang 80 Tài liệu dạy – học Toán 9 tập 2 timdapan.com"







