Bài 6 trang 54 SGK Hình học 11
Giải bài 6 trang 54 SGK Hình học 11. Cho bốn điểm A,B,C và D không đồng phẳng. Gọi M,N lần lượt là trung điểm của AC và BC. Trên đoạn BD lấy điểm P sao cho BP=2PD
Đề bài
Cho bốn điểm \(A,B,C\) và \(D\) không đồng phẳng. Gọi \(M,N\) lần lượt là trung điểm của \(AC\) và \(BC\). Trên đoạn \(BD\) lấy điểm \(P\) sao cho \(BP=2PD\).
a) Tìm giao điểm của đường thẳng \(CD\) và mặt phẳng \((MNP)\).
b) Tìm giao tuyến của hai mặt phẳng \((MNP)\) và \((ACD)\).
Phương pháp giải - Xem chi tiết
a) Gọi \(I\) là giao điểm của \(NP\) và \(CD\). Chứng minh \(I\) là giao điểm của đường thẳng \(CD\) và mặt phẳng \((MNP)\).
b) Tìm hai điểm chung của hai mặt phẳng \((MNP)\) và \((ACD)\).
Lời giải chi tiết
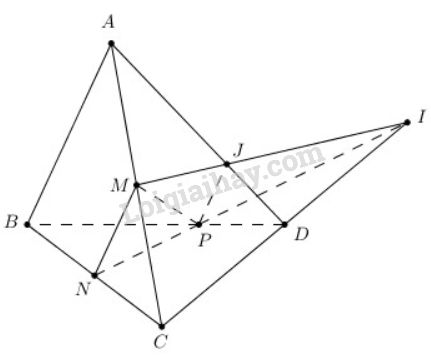
a) Trong \((BCD)\), gọi \(I\) là giao điểm của \(NP\) và \(CD\) \( \Rightarrow I \in CD\).
\(I\in NP\subset (MNP) \Rightarrow I \in \left( {MNP} \right)\).
Vậy \(CD\cap (MNP)=I\).
b) Trong \((ACD)\), gọi \(J=MI\cap AD\)
\(J\in AD\subset (ACD)\), \(M\in AC\subset (ACD) \Rightarrow MJ \subset \left( {ACD} \right)\).
Mà \(J \in MI \subset \left( {MNP} \right) \Rightarrow J \in \left( {MNP} \right)\)\( \Rightarrow MJ \subset \left( {MNP} \right)\).
Vậy \((MNP)\cap(ACD)=MJ\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 6 trang 54 SGK Hình học 11 timdapan.com"







