Bài 4 trang 34 SGK Hình học 11

Đề bài

Cho vectơ \( \overrightarrow{v}\), đường thẳng \(d\) vuông góc với giá của vectơ \( \overrightarrow{v}\). Gọi \(d'\) là ảnh của \(d\) qua phép tịnh tiến theo vectơ \( \dfrac{1}{2}\) \( \overrightarrow{v}\). Chứng minh rằng phép tịnh tiến theo vectơ \( \overrightarrow{v}\) là kết quả của việc thực hiện liên tiếp phép đối xứng qua các đường thẳng \(d\) và \(d'\).

Lời giải chi tiết

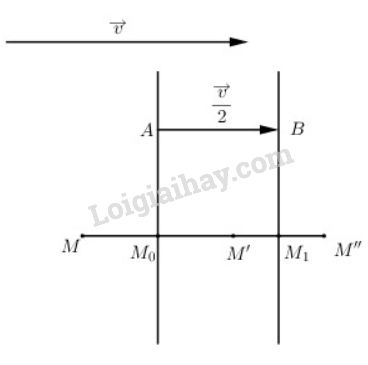
Lấy A bất kì thuộc đường thẳng d, xác định điểm B sao cho \(\overrightarrow {AB}  = {{\overrightarrow v } \over 2}\), qua B kẻ đường thẳng d’ // d. Khi đó d’ chính là ảnh của đường thẳng d qua phép tịnh tiến theo vector \({{\overrightarrow v } \over 2}\).

Lấy M là một điểm bất kì, gọi \(M' = {D_d}\left( M \right);\,\,M'' = {D_{d'}}\left( {M'} \right)\)

Gọi \({M_0} = MM' \cap d;\,\,{M_1} = M'M'' \cap d' \Rightarrow {M_0}\) và \({M_1}\) lần lượt là trung điểm của \(MM'\) và \(M'M''\).

Ta có \(\overrightarrow {MM'}  = 2\overrightarrow {{M_0}M'} ;\,\,\overrightarrow {M'M''}  = 2\overrightarrow {M'{M_1}} \)

\(\eqalign{  &  \Rightarrow \overrightarrow {MM''}  = \overrightarrow {MM'}  + \overrightarrow {M'M''}  = 2\overrightarrow {{M_0}M'}  + 2\overrightarrow {M'{M_1}}   \cr   & = 2\left( {\overrightarrow {{M_0}M'}  + \overrightarrow {M'{M_1}} } \right) = 2\overrightarrow {{M_0}{M_1}}  = 2\overrightarrow {AB}  \cr&= \overrightarrow v   \cr   &  \Rightarrow {T_{\overrightarrow v }}\left( M \right) = M'' \cr} \)

Vậy phép tịnh tiến theo vector \(\overrightarrow v \) là kết quả của việc thực hiện liên tiếp phép đối xứng qua các đường thẳng \(d\) và \(d'\).