Bài 3 trang 24 SGK Hình học 11
Giải bài 3 trang 24 SGK Hình học 11. Chứng minh rằng: Nếu một phép dời hình biến tam giác ABC thành tam giác A'B'C' thì nó cũng biến trọng tâm của tam giác ABC tương ứng thành trọng tâm của tam giác A'B'C'
Đề bài
Chứng minh rằng: Nếu một phép dời hình biến tam giác \(ABC\) thành tam giác \(A'B'C'\) thì nó cũng biến trọng tâm của tam giác \(ABC\) tương ứng thành trọng tâm của tam giác \(A'B'C'\)
Phương pháp giải - Xem chi tiết
Phép dời hình biến các đoạn thảng thành các đoạn thẳng, do đó biến các trung tuyến thành các trung tuyến tương ứng.
Lời giải chi tiết
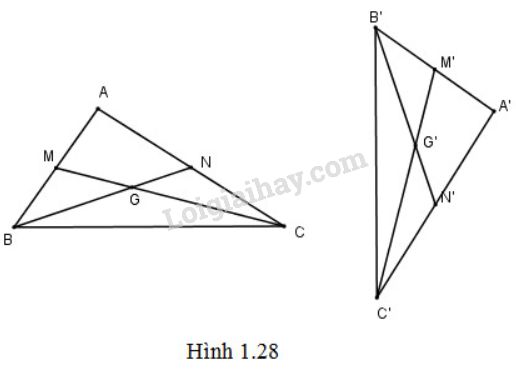
Gọi phép dời hình đó là \(f\). Do \(f\) biến các đoạn thẳng \(AB, AC\) tương ứng thành các đoạn thẳng \(A'B', A'C' \) nên nó cũng biến các trung điểm \(M, N\) của các đoạn thẳng \(AB, AC\) tương ứng theo thứ tự thành các trung điểm \(M', N'\) của các đoạn thẳng \(A'B', A'C'\). Vậy \(f\) biến các trung tuyến \(CM, BN\) của tam giác \(ABC\) tương ứng thành các trung tuyến \(C'M', B'N'\) của tam giác \(A'B'C'\). Từ đó suy ra \(f\) biến trọng tâm \(G\) của tam giác \(ABC\) của \(CM\) và \(BN\) thành trọng tâm \(G'\) của tam giác \(A'B'C'\) là giao của \(C'M'\) và \(B'N'\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 3 trang 24 SGK Hình học 11 timdapan.com"