Bài 10 trang 28 SGK Hình học 12

Đề bài

Cho hình hộp \(ABCD.A'B'C'D'\), gọi \(O\) là giao điểm của \(AC\) và \(BD\).

Tỉ số thể tích của khối chóp \(O.A'B'C'D'\) và khối hộp \(ABCD.A'B'C'D'\) bằng:

(A) \({1 \over 2}\)            (B) \({1 \over 3}\)                 (C) \({1 \over 4}\)                   (D) \({1 \over 6}\)

Lời giải chi tiết

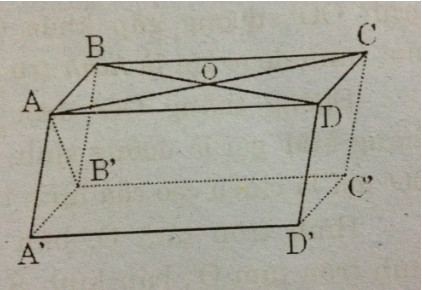
Dễ thấy khối chóp \(O.A'B'C'D'\) và khối hộp \(ABCD.A'B'C'D'\) có cùng chiều cao, gọi chiều cao của chúng bằng \(h\).

Ta có: \(\frac{{{V_{O.A'B'C'D'}}}}{{{V_{ABCD.A'B'C'D'}}}} = \frac{{\frac{1}{3}.{S_{A'B'C'D'}}.h}}{{{S_{A'B'C'D'}}.h}} = \frac{1}{3}\)

Chọn (B).