Đề thi khảo sát chất lượng lớp 9 môn Toán Sở GD&ĐT Vĩnh Phúc năm học

Đề khảo sát chất lượng lớp 9 môn Toán Sở GD&ĐT Vĩnh Phúc năm 2020

Đề thi khảo sát chất lượng lớp 9 môn Toán Sở GD&ĐT Vĩnh Phúc năm học 2019 - 2020 được thư viện đề thi Tìm Đáp Án đăng tải. Đây là đề kiểm tra KSCL môn Toán lớp 9 dành cho các bạn học sinh ôn tập, củng cố kiến thức, rèn luyện kĩ năng làm bài Toán. Mời các bạn cùng tham khảo

Đề thi học kì 2 lớp 9 môn Văn Sở GD&ĐT Nam Định năm học 2019 - 2020

Đề thi KSCL lớp 9 môn Toán trường THCS Trên Mây năm học 2019 - 2020
Đề thi KSCL lớp 9 môn Toán trường THCS Nam Từ Liêm năm học 2019 - 2020
Đề thi khảo sát chất lượng lớp 9 môn Toán Phòng GD&ĐT Long Biên năm học 2019 - 2020
Đề thi KSCL lớp 9 môn Toán Sở GD&ĐT Bắc Ninh năm học 2019 - 2020

SỞ GD&ĐT VĨNH PHÚC

ĐỀ CHÍNH THỨC

KHẢO SÁT CHẤT LƯỢNG HỌC KỲ II

NĂM HỌC 2019 - 2020

MÔN TOÁN - LỚP 9

Thời gian làm bài: 90 phút (Không kể thời gian giao đề)

Mã đề: 003 (Thí sinh làm bài ra tờ giấy thi và ghi rõ mã đề thi).

I. PHẦN TRẮC NGHIỆM (3,0 điểm)

Hãy viết vào tờ giấy thi chữ cái in hoa trước đáp án đúng.

Câu 1: Nghiệm của hệ phương trình: $\left\{ \matrix{ x - y = 2 \hfill \cr x+2y = -1 \hfill \cr} \right.$

A. (x; y) = (-1; 1).

B. (x; y) = (1; -1).

C. (x; y) = (2; 0).

D. (x; y) = (-1; 0).

Câu 2: Phương trình bậc hai $-2x² + 8x - 1 = 0$ có tổng hai nghiệm bằng

A. 4.

B. -4.

C. -2.

D. -1.

Câu 3: Phương trình bậc hai $x² + 5x - 1 = 0$ có biệt thức △ bằng

A. 6.

B. 14.

C. 21.

D. 29.

Câu 4: Cho đường tròn (O; 8 cm). Khi đó độ dài đường tròn bằng

A. 64π cm

B. 16π cm².

C. 16π cm.

D. 8π cm².

Câu 5: Một hình quạt tròn có bán kính 8cm, số đo cung là 36°. Khi đó diện tích hình quạt tròn bằng

A. 6,4π cm²

B. 0,8π cm².

C. 12,8π cm²

D. 1,6π cm²

Câu 6: Độ dài cung 60° của một đường tròn có bán kính 12 cm là

A. 9π cm

B. 4π cm.

C. 6π cm.

D. 3π cm.

II. PHẦN TỰ LUẬN (7,0 điểm)

Câu 7: (1,5 điểm)

a) Giải hệ phương trình: $\left\{ \matrix{ 2x - y = 3 \hfill \cr x + y = 0 \hfill \cr} \right.$

b) Giải phương trình: $x^4 +x^2-6=0.$

Câu 8: (1,0 điểm) Cho phương trình $x² – 2mx + m - 2 = 0 (1)$ . (x là ẩn, m là tham số)

a) Giải phương trình (1) khi m =1.

b) Chứng minh rằng phương trình (1) có nghiệm với mọi m.

Câu 9: (1,5 điểm) Theo kế hoạch trong tháng 3 năm 2020, hai tổ công nhân dự kiến may 7000 chiếc khẩu trang để phục vụ cho công tác phòng chống dịch Covid-19. Nhưng thực tế tổ I đã may vượt mức kế hoạch 10%, tổ II may vượt mức kế hoạch 12% nên cả hai tô đã may được 7780 chiếc khẩu trang. Hỏi theo kế hoạch mỗi tổ phải may bao nhiêu chiếc khẩu trang?

Câu 10: (2,5 điểm) Từ điểm M nằm ngoài đường tròn (O) kẻ hai tiếp tuyến MA, MB với đường tròn (O) (A, B là các tiếp điểm). Lấy điểm N bất kỳ trên cung nhỏ AB (không trùng với A, B). Gọi H, I, K lần lượt là chân đường vuông góc kẻ từ N đến các đường thẳng AM, AB, MB.

a) Chứng minh AHNI là tứ giác nội tiếp.

b) Chứng minh $∠NIH = ∠NBA.$

c) Gọi giao điểm của HI và AN là P, KI và NB là Q. Chứng minh PQ song song với AB.

Câu 11: (0,5 điểm) Cho a, b, c là các số thực dương thỏa mãn a + b + c = 3. Chứng minh rằng

$\dfrac{a^2(b+1)}{a+b + ab} + \dfrac{b^2(c+1)}{b + c+bc} + \dfrac{c^2(a+1)}{c+a+ca} ≥ 2$

Hết

Đáp án đề thi khảo sát chất lượng lớp 9 môn Toán Sở GD&ĐT Vĩnh Phúc năm 2020

I. PHẦN TRẮC NGHIỆM

Câu 1: B

Câu 2: A

Câu 3: D

Câu 4: C

Câu 5: A

Câu 6: B

II. PHẦN TỰ LUẬN

Câu 7:

$a)\ \left\{ \matrix{ 2x - y = 3 \hfill \cr x + y = 0 \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ x=1 \hfill \cr y=-1 \hfill \cr} \right.$

$b)\ x^4 +x^2-6=0$

$\Leftrightarrow \left[ \matrix{ x^2=2 \hfill \cr x^2=-3 \hfill \cr} \right.$

Vì $x^2 \geq 0 \Rightarrow x = ± \sqrt 2.$

Câu 8:

Thay m = 1 vào (1) ta có:

$x^2 – 2x +1 - 2 = 0$

$\Leftrightarrow \left[ \matrix{ x = 1+ \sqrt 2 \hfill \cr x = 1- \sqrt 2 \hfill \cr} \right.$

Ta có $\Delta' = m^2 - m + 2 = \left( m - \dfrac{1}2\right)^2 + \dfrac{7}4 >0$ với mọi m

Suy ra phương trình (1) luôn có nghiệm (đpcm).

Câu 9:

Theo kế hoạch mỗi tổ phải may số khẩu trang lần lượt là X và Y (chiếc, X,Y > 0)

Theo bài ra ta có hệ:

$\left\{ \matrix{ X+Y = 7000 \hfill \cr 1,1X + 1,12Y = 7780\hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ x=3000 \hfill \cr y=4000 \hfill \cr} \right.$

Câu 10:

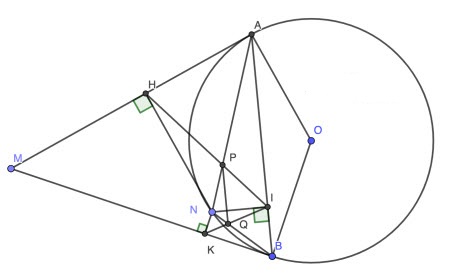
Đề thi khảo sát chất lượng lớp 9 môn Toán Sở GD&ĐT Vĩnh Phúc năm học 2019 - 2020

Theo giả thiết ta có $∠NHA = ∠NIA = 90° ⇒ H, I$ cùng thuộc đường tròn đường kính NA hay AHNI là tứ giác nội tiếp (đpcm).

Vì AHNI là tứ giác nội tiếp $⇒ ∠NIH = ∠NAH$ (góc nội tiếp cùng chắn cung NH)

Lại có $∠NAH = ∠NBA$ (t/c góc tạo bởi tiếp tuyến và dây cung)

Suy ra $∠NIH = ∠NBA (đpcm).$

Vì AHNI là tứ giác nội tiếp $⇒ ∠PIN = ∠NAH = ∠NBA (cmt)$

tương tự ta chứng minh được NIBK nội tiếp $⇒ ∠NIQ = ∠NBK = ∠NAB.$

Ta có:

$∠PIQ = ∠PIN + ∠NIQ = ∠NBA + ∠NAB = 180° - ∠ANB$

hay $∠PIQ + ∠PNQ = 180° ⇒$ Tứ giác NPIQ nội tiếp.

$⇒ ∠NPQ = ∠NIQ = ∠NAB ⇒ PQ // AB$ (góc tạo bởi vị trí đồng vị) (đpcm).

Câu 11:

Áp dụng BĐT Bunhya - Copxki cho 2 bộ số $\left( \dfrac{a_1}{\sqrt {b_1}}; \dfrac{a_2}{\sqrt {b_2}}; \dfrac{a_3}{\sqrt {b_3}} \right) và \left( \sqrt{b_1}; \sqrt{b_2}; \sqrt{b_3} \right),$ ta có:

$({b_1+b_2+b_3})\left(\dfrac{a_1^2}{b_1} + \dfrac{a_2^2}{b_2} + \dfrac{a_3^2}{b_3} \right) \geq (a_1+a_2+a_3)^2$

Suy ra được BĐT Svac-Xơ có dạng:

$\dfrac{a_1^2}{b_1} + \dfrac{a_2^2}{b_2} + \dfrac{a_3^2}{b_3} \geq \dfrac{(a_1+a_2+a_3)^2}{b_1+b_2+b_3} (1)$

Ta có:

$\dfrac{a^2(b+1)}{a+b + ab} = \dfrac{a^2(b+1)}{b+a(b+1)} =\dfrac{a^2}{a+\dfrac{b}{b+1}}$

Áp dụng (1), ta có:

$\dfrac{a^2(b+1)}{a+b + ab} + \dfrac{b^2(c+1)}{b + c+bc} + \dfrac{c^2(a+1)}{c+a+ca}$

$=\dfrac{a^2}{a+\dfrac{b}{b+1}} + \dfrac{b^2}{b+\dfrac{c}{c+1}} + \dfrac{c^2}{c+\dfrac{a}{a+1}} \geq \dfrac{(a+b+c)^2}{a+b+c+\dfrac{a}{a+1}+\dfrac{b}{b+1}+\dfrac{c}{c+1}} (*)$

Ta có:

$\dfrac{(a+b+c)^2}{a+b+c+\dfrac{a}{a+1}+\dfrac{b}{b+1}+\dfrac{c}{c+1}} = \dfrac{9}{3+1- \dfrac{1}{a+1}+1-\dfrac{1}{b+1}+1-\dfrac{1}{c+1}}$

$= \dfrac{9}{6- \dfrac{1}{a+1}-\dfrac{1}{b+1}-\dfrac{1}{c+1}}$

Tiếp tục áp dụng (1), ta có:

$\dfrac{1}{a+1}+\dfrac{1}{b+1}+\dfrac{1}{c+1} \geq \dfrac{(1+1+1)^2}{a+1+b+1+c+1} = \dfrac{3}{2}$

$\Leftrightarrow 6 - \dfrac{1}{a+1}-\dfrac{1}{b+1}-\dfrac{1}{c+1} \leq \dfrac{9}{2}$

$\Leftrightarrow \dfrac{9}{6- \dfrac{1}{a+1}-\dfrac{1}{b+1}-\dfrac{1}{c+1}} \geq 2$

(vì $6 - \dfrac{1}{a+1}-\dfrac{1}{b+1}-\dfrac{1}{c+1} =\Sigma a + \Sigma\left(\dfrac{a}{a+1}\right)>0$ )

$\Leftrightarrow \dfrac{(a+b+c)^2}{a+b+c+\dfrac{a}{a+1}+\dfrac{b}{b+1}+\dfrac{c}{c+1}} \geq 2 (**)$

Từ (*) và (**) ta có:

$\dfrac{a^2(b+1)}{a+b + ab} + \dfrac{b^2(c+1)}{b + c+bc} + \dfrac{c^2(a+1)}{c+a+ca} \geq 2 (đpcm)$

Dấu bằng xảy ra khi và chỉ khi a = b = c = 1.

Đề thi khảo sát chất lượng lớp 9 môn Toán Sở GD&ĐT Vĩnh Phúc năm học 2019 - 2020. Đề thi gồm 5 câu hỏi tự luận với 120 phút làm bài kèm theo đáp án được TimDapAnchia sẻ giúp các bạn học sinh ôn tập, biết cách phân bổ thời gian làm bài. Mời các bạn cùng tham khảo

.......................................................................

Ngoài Đề thi khảo sát chất lượng lớp 9 môn Toán Sở GD&ĐT Vĩnh Phúc năm học 2019 - 2020. Mời các bạn học sinh còn có thể tham khảo các đề thi học học kì 1 lớp 9, đề thi học học kì 2 lớp 9 các môn Toán, Văn, Anh, Hóa, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với đề thi học kì 1, 2 lớp 9 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn ôn thi tốt

Nếu bạn không thấy đề thi được hiển thị. Vui lòng tải về để xem. Nếu thấy hay thì các bạn đừng quên chia sẻ cho bạn bè nhé!

Tải về