Đề thi khảo sát chất lượng lớp 9 môn Toán Sở GD&ĐT Nam Định năm học

Đề khảo sát chất lượng lớp 9 môn Toán Sở GD&ĐT Nam Định năm 2020

Đề thi khảo sát chất lượng lớp 9 môn Toán Sở GD&ĐT Nam Định năm học 2019 - 2020 được TimDapAnsưu tầm và đăng tải. Đây là đề kiểm tra KSCL môn Toán lớp 9 dành cho các bạn học sinh ôn tập, củng cố kiến thức, rèn luyện kĩ năng làm bài Toán. Mời các bạn cùng tham khảo

Đề thi KSCL lớp 9 môn Toán trường THCS Trên Mây năm học 2019 - 2020
Đề thi KSCL lớp 9 môn Toán trường THCS Nam Từ Liêm năm học 2019 - 2020
Đề thi khảo sát chất lượng lớp 9 môn Toán Phòng GD&ĐT Long Biên năm học 2019 - 2020
Đề thi KSCL lớp 9 môn Toán Sở GD&ĐT Bắc Ninh năm học 2019 - 2020

Phần I Trắc nghiệm (2,0 điểm)

Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước phương án đó vào bài làm

Câu 1: Điều kiện để biểu thức $\sqrt{x-2020}$ xác định là

$A. x ≠2020$

$B. x>2020$

$C. x\geq2020$

$D. x\leq2020$

Câu 2: Hệ số góc của đường thẳng có phương trình $y= 2020x + 2021$ là

A. 2020

B. -2020

C. 2021

D. 4041

Câu 3: Tìm tất cả các giá trị của tham số m để hàm số $y = (3 - m)x + 2019$ nghịch biến trên ℝ

A. m<3

$B. m\geq3$

C. m<0

D. m>3

Câu 4: Trong mặt phẳng tọa độ Oxy, đồ thị hàm số $y=10x^2$ đi qua điểm

A. M(1:10).

B. N(-1:-10).

C. P(10; 1).

D. Q(10,-1).

Câu 5: Phương trình $x^2+x-2020m=0$ có hai nghiệm trái dấu khi và chỉ khi

A. m<0

B. m>0

$C. m\geq0$

$D. m\leq0$

Câu 6: Cho hình tròn (O, R) có diện tích bằng $100\pi \space {cm}^3$ . Chu vi của đường tròn đó bằng

$A. 100\pi \space {cm}$

$B. 10\pi \space {cm}$

$C.\ 20\pi \space {cm}$

$D. 20\space {cm}$

Câu 7: Một quả bóng hình cầu có thể tích bằng $288\pi \space {cm}^3$ . Bán kính của quả bóng đó bằng

A. 3 cm

B. 9 cm

$C. 6\sqrt 2 \space cm$

D. 6cm

Câu 8. Một máy bay đang bay ở độ cao 10 km (so với mặt đất). Khi hạ cánh xuống mặt đất, giả sử đường đi của máy bay là một đường thẳng và tạo với mặt đất một góc nghiêng là a. Tại vị trí máy bay đang cách sân bay 57,6 km phi công bắt đầu cho máy bay hạ cánh. Hãy tỉnh góc nghiêng a (kết quả làm tròn đến độ)?

A. a= 9°

B. a = 10°

C. a=11°

D. a =12°

Phần II. Tự luận (8,0 điểm)

Câu 1. (1,5 điểm)

1) Chứng minh đẳng thức:

$\sqrt{7+4\sqrt3} + \sqrt{7-4\sqrt3} =4$

2) Rút gọn biểu thức:

$Q= \dfrac{\sqrt x -1}{x^2-x}: \left( \dfrac{1}{\sqrt x}- \dfrac{1}{\sqrt x+1} \right)$ với x> 0; x ≠ 1

Câu 2. (1,5 điểm)

Cho phương trình $x^2-3x+m=0 (1)$ với m là tham số, .

1) Giải phương trình (1) khi m =1.

2) Tìm tất cả các giá trị của tham số m để phương trình (1) có hai nghiệm phân biệt $x_1;x_2$ thỏa mãn

$x_1^2+x_2^2 = 2020$

Câu 3. (1,0 điểm) Giải hệ phương trình:

$\left\{ \matrix{ 2\sqrt{x+1} + \dfrac{3}{y-1} = 5 \hfill \cr 3\sqrt{x+1} + \dfrac{2}{y-1} = 5 \hfill \cr} \right.$

Câu 4. (3,0 điểm)

Cho tam giác ABC có ba góc nhọn (AB < AC) nội tiếp đường tròn (O). Gọi H là trực tâm và M, N, P lần lượt là chân đường cao kẻ từ các đỉnh A, B, C của tam giác ABC.

1) Chứng minh các tứ giác APHN và BPNC là các tứ giác nội tiếp.

2) Chứng minh điểm H là tâm đường tròn nội tiếp tam giác MNP.

3) Chứng minh đường thẳng OA vuông góc với đường thẳng NP.

Câu 5. (1,0 điểm)

1) Giải phương trình $\sqrt{x-2} + \sqrt{10-x}=(x-6)^2 (x - 2)(10 - x) +4$

2) Xét các số a, b, c thay đổi thỏa mãn

$a\left(a - \dfrac{2021}{3} \right) + b\left(b - \dfrac{2021}{3} \right) + c\left(c - \dfrac{2021}{3} \right) + \dfrac{2020}{3} \leq 0$

Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức $S = a + b + c.$

Hết

Đáp án đề thi khảo sát chất lượng lớp 9 môn Toán Sở GD&ĐT Nam Định năm 2020

Phần I. Trắc nghiệm

Câu 1	C	Câu 5	B
Câu 2	A	Câu 6	C
Câu 3	D	Câu 7	D
Câu 4	A	Câu 8	B

Phần II. Tự luận (8,0 điểm)

Câu 1. (1,5 điểm)

1) Ta có:

$VT = \sqrt{7+4\sqrt3} + \sqrt{7-4\sqrt3}$

$= \sqrt{4+2.2\sqrt3+3 }+ \sqrt{4-2.2\sqrt3+3}$

$= \sqrt{(2+\sqrt3)^2} + \sqrt{(2-\sqrt3)^2}$

$= (2+\sqrt3) + (2-\sqrt3) = 4 (đpcm).$

Với x> 0; x ≠ 1, ta có:

$Q= \dfrac{\sqrt x -1}{x^2-x}: \left( \dfrac{1}{\sqrt x}- \dfrac{1}{\sqrt x+1} \right)$

$= \dfrac{\sqrt x -1}{x(\sqrt x-1)(\sqrt x+1)}: \dfrac{1}{\sqrt x(\sqrt x+1)}$

$= \dfrac{1}{x(\sqrt x+1)}.{\sqrt x(\sqrt x+1)} = \dfrac{1}{\sqrt x}.$

Câu 2. (1,5 điểm)

Cho phương trình $x^2-3x+m=0\ (1)$ với m là tham số, .

Thay m = 1 vào (1), ta có:

$(1) ⇔ x^2-3x+1=0$

$⇔ \left[ \matrix{ {x} = \dfrac{3+\sqrt 5}{2} \hfill \cr {x} = \dfrac{3-\sqrt 5}{2} \hfill \cr} \right.$

2) Để phương trình (1) có hai nghiệm phân biệt khi và chỉ khi:

$\Delta = 3^2 - 4m = 9 - 4m > 0 ⇔ m < \dfrac{9}{4}$

Áp dụng hệ thức Vi-ét vào phương trình (1), ta có:

$\left\{ \matrix{ x_1+x_2 = 3 \hfill \cr x_1x_2 = m \hfill \cr} \right.$

Ta có:

$x_1^2+x_2^2 = 2020$

$⇔ (x_1+x_2)^2 -2 x_1x_2= 2020$

$⇔ 3^2 -2 m= 2020$

$⇔ m = \dfrac{-2011}{2}$ (thoả mãn đk)

⇒ Kết luận.....

Câu 3. (1,0 điểm) Giải hệ phương trình:

$\left\{ \matrix{ 2\sqrt{x+1} + \dfrac{3}{y-1} = 5 \hfill \cr 3\sqrt{x+1} + \dfrac{2}{y-1} = 5 \hfill \cr} \right.$

$ĐKXĐ: x \geq -1; y≠1$

$⇔ \left\{ \matrix{ \sqrt{x+1} =1 \hfill \cr \dfrac{1}{y-1} = 1 \hfill \cr} \right.$

$⇔ \left\{ \matrix{x = 0 \hfill \cr y = 2 \hfill \cr} \right.$ (thoả mãn đkxđ)

⇒ Kết luận.....

Câu 4. (3,0 điểm)

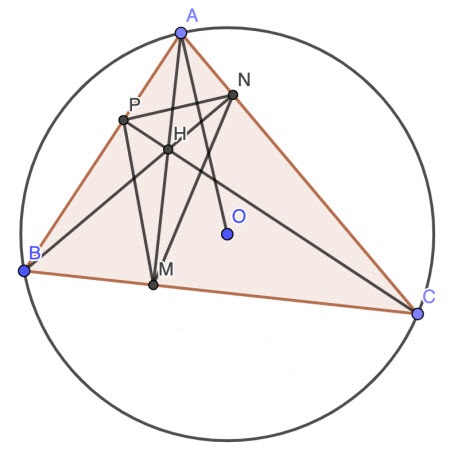
Đề thi khảo sát chất lượng lớp 9 môn Toán Sở GD&ĐT Nam Định năm học 2019 - 2020

Vì H là trực tâm và M, N, P lần lượt là chân đường cao kẻ từ các đỉnh A, B, C của tam giác $ABC ⇒ ∠APH = ∠ANH = 90° ⇒ P$ và N cùng thuộc đường tròn đường kính AH, hay tứ giác APHN là tứ giác nội tiếp (đpcm).

Tương tự ta có $∠BPC = ∠BNC = 90° ⇒ P$ và N cùng thuộc đường tròn đường kính BC, hay tứ giác BPNC là tứ giác nội tiếp (đpcm).

Vì tứ giác APHN là tứ giác nội tiếp ⇒ ∠HPN = ∠HAN (Góc nội tiếp (ABHN) cùng chắn cung HN)

Tương tự ý trên, ta chứng minh được các tứ giác BPHM và CNHM nội tiếp.

$⇒ ∠HPM = ∠HBM = 90° - ∠BHM = 90° - ∠AHN = ∠HAN = ∠HPN$

Hay PH là phân giác trong của góc NPM.

Chứng minh tương tự ta có: $∠PNH = ∠HNM ⇒ PH$ là phân giác trong của góc PNM.

Hay H là giao của ba đường phân giác trong của tam giác MNP, hay H là tâm đường tròn nội tiếp tam giác MNP (đpcm).

3) Chứng minh đường thẳng OA vuông góc với đường thẳng NP.

Vì tứ giác BPNC nội tiếp $(cmt) ⇒ ∠ACB = ∠NCB = 180° - ∠NPB = ∠APN (1)$

Ta lại có: $∠PAO = 90° - ∠AOB/2 = 90° - ∠ACB (2)$

Từ (1) và (2) ta có: $∠PAO + ∠APN = 90° ⇒ AO ⊥ PN (đpcm).$

Câu 5. (1,0 điểm)

1) Giải phương trình $\sqrt{x-2} + \sqrt{10-x}=(x-6)^2 (x - 2)(10 - x) +4 (1)$

$ĐKXĐ: 2 \leq x \leq 10$

Ta có $2 \leq x \leq 10$

$\Rightarrow (x-6)^2 (x - 2)(10 - x) \geq 0$

$\Rightarrow VP(1) = (x-6)^2 (x - 2)(10 - x) + 4 \geq 4 (*)$

Áp dụng BĐT Bunhya Cốp-xki, ta có:

$VT (1) = 1.\sqrt{x-2} + 1.\sqrt{10-x} \leq \sqrt{(1+1)(x-2+10-x)} = 4 (**)$

Từ (*) và (**) ta có:

$VT (1) = 1.\sqrt{x-2} + 1.\sqrt{10-x} \leq 4 \leq (x-6)^2 (x - 2)(10 - x) + 4 = VP(1)$

Vậy (1) xảy ra $\Leftrightarrow VT(1) = VP(1) = 4$

$\Leftrightarrow \left\{ \matrix{ (x-6)^2 (x - 2)(10 - x) = 0 \hfill \cr \sqrt{x-2} = \sqrt{10-x} \hfill \cr} \right.$

$\Leftrightarrow x=6$

Kết luận ......

2) Ta có:

$a\left(a - \dfrac{2021}{3} \right) + b\left(b - \dfrac{2021}{3} \right) + c\left(c - \dfrac{2021}{3} \right) + \dfrac{2020}{3} \leq 0$

$\Leftrightarrow a^2+b^2+c^2 - \dfrac{2021}{3} (a+b+c)+ \dfrac{2020}{3} \leq 0$

Áp dụng BĐT quen thuộc:

$a^2+b^2+c^2 \geq \dfrac{1}{3}(a+b+c)^2$

$\Leftrightarrow \dfrac{1}{3} (a+b+c)^2 - \dfrac{2021}{3} (a+b+c)+ \dfrac{2020}{3} \leq a^2+b^2+c^2 - \dfrac{2021}{3} (a+b+c)+ \dfrac{2020}{3} \leq 0$

$\Leftrightarrow (a+b+c)^2 -{2021}(a+b+c)+ {2020} \leq 0$

$\Leftrightarrow (a+b+c - 1)(a+b+c-2020) \leq 0$

$\Leftrightarrow 1 \leq S \leq 2020$

Vậy ${min} _S = 1 \Leftrightarrow a=b=c= \dfrac{1}{3}$

${max} _S = 2020 \Leftrightarrow a=b=c= \dfrac{2020}{3}.$

Đề thi khảo sát chất lượng lớp 9 môn Toán Sở GD&ĐT Nam Định năm học 2019 - 2020. Đề thi gồm 8 câu hỏi trắc nghiệm, 5 câu hỏi tự luận với 120 phút làm bài kèm theo đáp án được TimDapAnchia sẻ giúp các bạn học sinh ôn tập, biết cách phân bổ thời gian làm bài. Mời các bạn cùng tham khảo

Đề thi khảo sát chất lượng lớp 9 môn Toán Phòng GD&ĐT Hà Đông năm học 2019 - 2020
Đề thi khảo sát chất lượng lớp 9 môn Toán Phòng GD&ĐT Thạch Thất năm học 2019 - 2020
Đề thi khảo sát chất lượng lớp 9 môn Toán Phòng GD&ĐT Ba Đình năm học 2019 - 2020
Đề thi khảo sát chất lượng lớp 9 môn Toán Phòng GD&ĐT Mê Linh năm học 2019 - 2020 (đợt 2)
Đề thi khảo sát chất lượng lớp 9 môn Toán Sở GD&ĐT Hà Nam năm học 2019 - 2020

.......................................................................

Ngoài Đề thi khảo sát chất lượng lớp 9 môn Toán Sở GD&ĐT Nam Định năm học 2019 - 2020. Mời các bạn học sinh còn có thể tham khảo các đề thi học học kì 1 lớp 9, đề thi học học kì 2 lớp 9 các môn Toán, Văn, Anh, Hóa, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với đề thi học kì 1, 2 lớp 9 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn ôn thi tốt

Nếu bạn không thấy đề thi được hiển thị. Vui lòng tải về để xem. Nếu thấy hay thì các bạn đừng quên chia sẻ cho bạn bè nhé!

Tải về