Lý thuyết hàm số y = ax + b

1. Định nghĩa

Hàm số bậc nhất là hàm số có công thức: \(y = ax + b\) trong đó \(a\) và \(b\) là các số đã cho với \(a ≠ 0, x\) là biến số.

2. Sự biến thiên

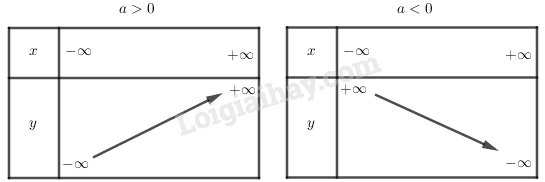
Hàm số bậc nhất \(y = ax + b (a ≠ 0)\) có tập xác định \(D =\mathbb R\), đồng biến trên \(\mathbb R\) nếu \(a > 0\) và nghịch biến trên \(\mathbb R\) nếu \(a < 0\).

Bảng biến thiên của hàm số bậc nhất tùy theo \(a\) như sau:

3. Đồ thị

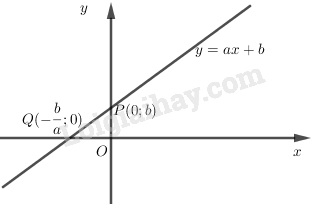
Đồ thị hàm số \(y = ax + b (a ≠ 0)\) là một đường thẳng không song song cũng không trùng với các trục tọa độ, cắt trục tung tại điểm \(P(0; b)\) và cắt trục hoành tại điểm \(Q = \left( { - {b \over a};0} \right)\)

Ta gọi đồ thị của hàm số \(y = ax + b\) là đường thẳng \(y=ax + b\). Số \(a\) gọi là hệ số góc của đường thẳng \(y = ax + b\).

4. Hàm số hằng \(y = b\)

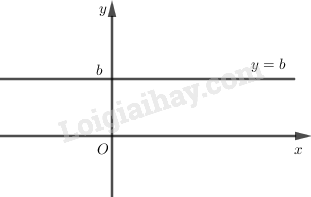
Khi \(a = 0\) hàm số \(y = ax + b\) trở thành hàm hằng \(y = b\) là đường thẳng song song với trục hoành cắt trục tung tại điểm \(P(0; b)\). Ta gọi đường thẳng này là đường thẳng \(y = b\). 

5. Hàm số \(y = |x|\)

\(y = |x| = \left\{ \matrix{
x,\text { nếu }x \ge 0 \hfill \cr
- x,\text { nếu }x < 0 \hfill \cr} \right.\)

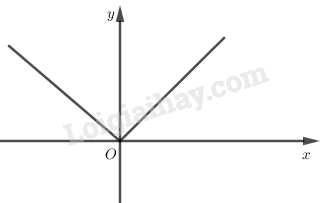
có tập xác định \(D =\mathbb R\), đồng biến trên khoảng \((0; +∞)\) và nghịch biến trên khoảng \((- ∞; 0)\).

Đồ thị là đường thẳng; trên nửa khoảng \([0; +∞)\) trùng với đồ thị hàm số \(y = x\) và trên khoảng \((- ∞; 0)\) trùng với đồ thị hàm số \(y = - x\).