Bài 1 trang 41 SGK Đại số 10
Giải bài 1 trang 41 SGK Đại số 10. Vẽ đồ thị hàm số.
Vẽ đồ thị hàm số:
LG a
\(y = 2x - 3\);
Phương pháp giải:
Đồ thị của hàm số y = ax + b là một đường thẳng không song song và cũng không trùng với các trục tọa độ. Đường thẳng này luôn đi qua hai điểm \(A\left( {0;b} \right);B\left( { - \frac{b}{a};0} \right)\)
Lời giải chi tiết:
Đồ thị hàm số \(y = 2x - 3\) là đường thẳng đi qua hai điểm \(A(0; - 3)\) và \(B=\left ( \frac{3}{2};0 \right )\)
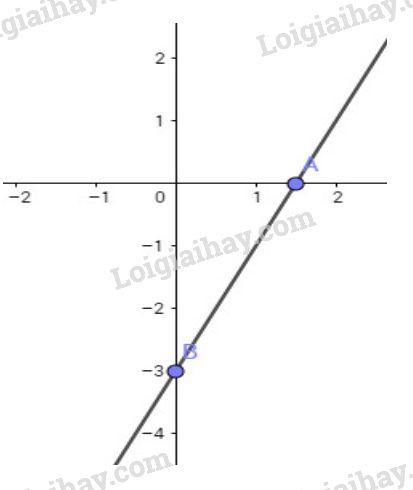
LG b
\(y = \sqrt 2\);
Phương pháp giải:
Đồ thị của hàm số y = ax + b là một đường thẳng không song song và cũng không trùng với các trục tọa độ. Đường thẳng này luôn đi qua hai điểm \(A\left( {0;b} \right);B\left( { - \frac{b}{a};0} \right)\)
Lời giải chi tiết:
Đồ thị hàm số \(y = \sqrt 2\) là đường thẳng song song với trục hoành đi qua điểm \(A(0; \sqrt 2)\)

LG c
\(y=-\frac{3x}{2}+7;\)
Phương pháp giải:
Đồ thị của hàm số y = ax + b là một đường thẳng không song song và cũng không trùng với các trục tọa độ. Đường thẳng này luôn đi qua hai điểm \(A\left( {0;b} \right);B\left( { - \frac{b}{a};0} \right)\)
Lời giải chi tiết:
Đồ thị hàm số \(y=-\frac{3x}{2}+7\) là đường thẳng. Bởi vì giao điểm của đồ thị với trục tung \(P(0; 7)\) với trục hoành \(Q=(\frac{14}{3};0)\) có tọa độ tương đối lớn nên ta có thể chọn các điểm thuộc đồ thị có tọa độ nhỏ hơn cho dễ vẽ. Chẳng hạn \(A(4; 1), B(2; 4)\). Đồ thị là đường thẳng AB
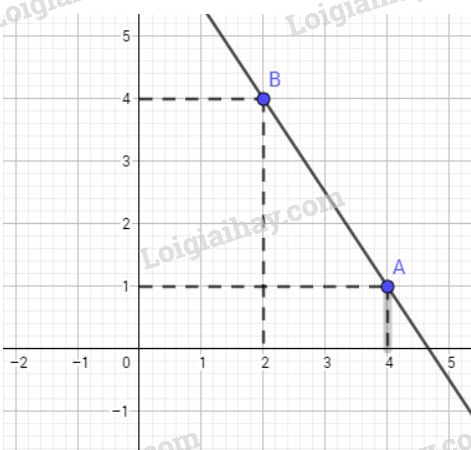
LG d
\(y = |x|\).
Phương pháp giải:
Đồ thị của hàm số y = ax + b là một đường thẳng không song song và cũng không trùng với các trục tọa độ. Đường thẳng này luôn đi qua hai điểm \(A\left( {0;b} \right);B\left( { - \frac{b}{a};0} \right)\)
Lời giải chi tiết:
\(y = |x| - 1 = \left\{ \matrix{
x - 1,x \ge 0 \hfill \cr
- x - 1,x < 0 \hfill \cr} \right.\)
Ta vẽ hai đường thẳng \(y=x-1\) với \(x\ge0\) và đường thẳng \(y=-x-1\) với \(x<0\)
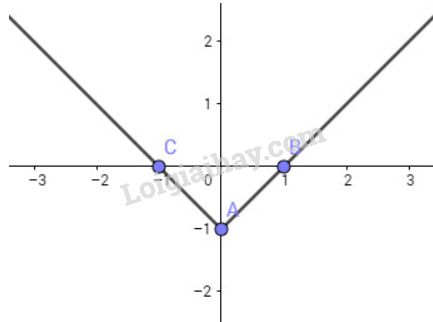
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 1 trang 41 SGK Đại số 10 timdapan.com"







