Lý thuyết hàm số bậc hai
Hàm số bậc hai được cho bởi công thức.
1. Hàm số bậc hai là hàm số có công thức: \(y = ax^2 + bx + c (a ≠ 0)\) có miền xác định \(D =\mathbb R\), biệt thức \(\Delta = {b^2} - 4ac\)
Bảng biến thiên:

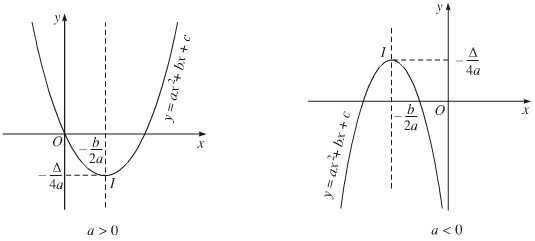
Đồ thị hàm số \(y = ax^2+ bx + c (a ≠ 0)\) là đường thẳng parabol có: đỉnh \(I\left( { - {b \over {2{\rm{a}}}}; - {\Delta \over {4{\rm{a}}}}} \right)\), trục đối xứng là đường thẳng \(x = - {b \over {2{\rm{a}}}}\).
Giao điểm với trục : \(A(0; c)\). Hoành độ giao điểm với trục hoành là nghiệm của \(ax^2 + bx + c = 0\).
Đồ thị hàm số \(y = ax^2 + bx + c (a ≠ 0)\) suy ra từ đồ thị hàm số \(y = ax^2\) bằng cách:
+ Tịnh tiến song song với trục hoành \(\left| {{b \over {2{\rm{a}}}}} \right|\) đơn vị bên trái nếu \({b \over {2{\rm{a}}}}\) > 0, về bên phải nếu \({b \over {2{\rm{a}}}}\) < 0.
+ Tịnh tiến song song với trục tung \(\left| { - {\Delta \over {4{\rm{a}}}}} \right|\) đơn vị lên trên nếu \({ - {\Delta \over {4{\rm{a}}}}}\) > 0, và xuống dưới nếu \({ - {\Delta \over {4{\rm{a}}}}}\) < 0.
Search google: "từ khóa + timdapan.com" Ví dụ: "Lý thuyết hàm số bậc hai timdapan.com"







