Giải bài tập 2 trang 82 SGK Toán 9 tập 1 - Chân trời sáng tạo
Cho hình chữ nhật ABCD có AD = 18 cm và CD = 12 cm. Chứng minh rằng bốn điểm A, B, C, D cùng thuộc một đường tròn. Tính bán kính của đường tròn đó.
Đề bài
Cho hình chữ nhật ABCD có AD = 18 cm và CD = 12 cm. Chứng minh rằng bốn điểm A, B, C, D cùng thuộc một đường tròn. Tính bán kính của đường tròn đó.
Phương pháp giải - Xem chi tiết
- Đọc kĩ dữ liệu đề bài để vẽ hình
- Áp dụng khoảng cách từ tâm đến đường tròn để chứng minh 4 điểm thuộc đường tròn
- Bán kính đường tròn bằng nửa đường chéo hình chữ nhật.
Lời giải chi tiết
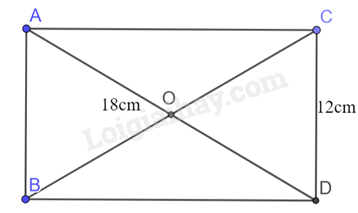
Ta có ABCD là hình chữ nhật và gọi O là giao của hai đường chéo AD và CD.
Nên ta có OA = OB = OC = OD suy ra bốn điểm A, B, C, D cùng thuộc đường tròn tâm O, bán kính OA.
Ta có R = OA = \(\frac{{AD}}{2} = \frac{{18}}{2} = 9cm\).
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài tập 2 trang 82 SGK Toán 9 tập 1 - Chân trời sáng tạo timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài tập 2 trang 82 SGK Toán 9 tập 1 - Chân trời sáng tạo timdapan.com"







