Bài 96 trang 151 SBT toán 7 tập 1
Giải bài 96 trang 151 sách bài tập toán 7 tập 1. Cho tam giác ABC cân tại A. Các đường trung trực của AB, AC cắt nhau ở I. Chứng minh rằng AI là tia phân giác của góc A.
Đề bài
Cho tam giác \(ABC\) cân tại \(A.\) Các đường trung trực của \(AB, AC\) cắt nhau ở \(I.\) Chứng minh rằng \(AI\) là tia phân giác của góc \(A.\)
Phương pháp giải - Xem chi tiết
Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
Lời giải chi tiết
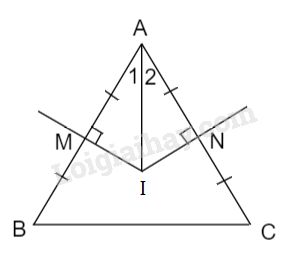
Giả sử \(IM, IN\) là hai đường trung trực của \(AB, AC.\)
Ta có:
\( AB{\rm{ }} = {\rm{ }}AC\) (vì \(\Delta ABC\) cân tại \(A\)) (1)
\(\displaystyle AM = {1 \over 2}AB\) (vì \(IM\) là trung trực của \(AB\)) (2)
\( \displaystyle AN = {1 \over 2}AC\) (vì \(IN\) là trung trực của \(AC\)) (3)
Từ (1), (2) và (3) suy ra: \(AM = AN\).
Xét hai tam giác vuông \(AMI\) và \(ANI\) có:
\(\widehat {AMI} = \widehat {ANI} = 90^\circ \)
\(AM = AN \) (chứng minh trên)
\(AI\) cạnh chung
\( \Rightarrow ∆AMI = ∆ANI\) (cạnh huyền - cạnh góc vuông).
\( \Rightarrow \widehat {{A_1}} = \widehat {{A_2}}\) (hai góc tương ứng).
Vậy \(AI\) là tia phân giác của \(\widehat {BAC}\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 96 trang 151 SBT toán 7 tập 1 timdapan.com"







