Bài 8.1, 8.2, 8.3 phần bài tập bổ sung trang 152 SBT toán 7 tập 1

Bài 8.1

Trong các khẳng định sau, khẳng định nào là đúng, khẳng định nào là sai ?

Các tam giác vuông \(ABC\) và \(DEF\) có \(\widehat A = \widehat D = {90^o},AC = DE\) bằng nhau nếu có thêm :

a) \(BC = EF\);

b) \(\widehat C = \widehat E\);

c) \(\widehat C = \widehat F\). 

Phương pháp giải:

- Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

- Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

Giải chi tiết:

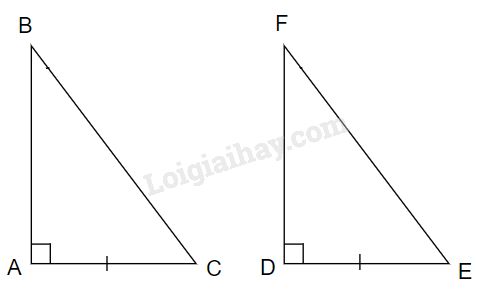
Xét hai tam giác vuông \(ABC\) và \(DFE\) có:

\(\widehat A = \widehat D = {90^o}\)

\(AC = DE\) 

a) Thêm điều kiện \(BC = EF\) thì \(\Delta ABC = \Delta DFE\) (cạnh huyền - cạnh góc vuông).

b) Thêm điều kiện \(\widehat C = \widehat E\) thì \(\Delta ABC = \Delta DFE\) (cạnh góc vuông - góc nhọn kề).

c) Thêm điều kiện \(\widehat C = \widehat F\) thì ta không thể kết luận \(\Delta ABC = \Delta DFE\).

Bài 8.2

Các tam giác vuông \(ABC\) và \(DEF\) có \(\widehat A = \widehat D = {90^o},AC = DF,\widehat B = \widehat E\). Các tam giác vuông có bằng nhau không? 

Phương pháp giải:

Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.

Giải chi tiết:

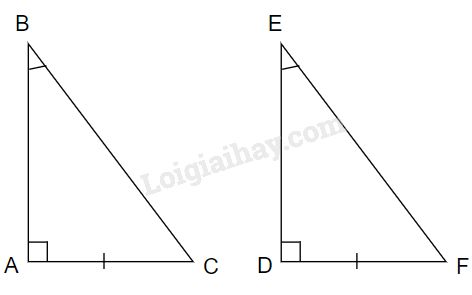
Áp dụng định lí tổng các góc của một tam giác vào \(\Delta ABC,\,\Delta DEF\) ta có:

\(\begin{array}{l} 
\widehat A + \widehat B + \widehat C = {180^o}\\
\widehat D + \widehat E + \widehat F = {180^o}\\
\Rightarrow \widehat A + \widehat B + \widehat C = \widehat D + \widehat E + \widehat F
\end{array}\)

Mà \(\widehat A = \widehat D = {90^o};\widehat B = \widehat E\,(gt)\)

\( \Rightarrow \widehat C = \widehat F\)

Xét \(\Delta ABC\) và \(\Delta DEF\) có:

\(\widehat A = \widehat D = {90^o}\)

\(AC=DF\) (gt)

\(\widehat C = \widehat F\) (chứng minh trên)

\( \Rightarrow ΔABC = ΔDEF\) (g.c.g).

Bài 8.3

Cho tam giác \(ABC\) cân tại \(A.\) Trên tia đối \(BC\) lấy điểm \(D\), Trên tia đối của tia \(CB\) lấy điểm \(E\) sao cho \(\widehat {BAD} = \widehat {CAE}\). Kẻ \(BH\) vuông góc với \(AD \;(H ∈ AD).\) Kẻ \(CK\) vuông góc với \(AE \;(K ∈ AE).\) Chứng minh rằng:

a) \(BD = CE\)

b) \(BH = CK\) 

Phương pháp giải:

- Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.

- Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

Giải chi tiết:

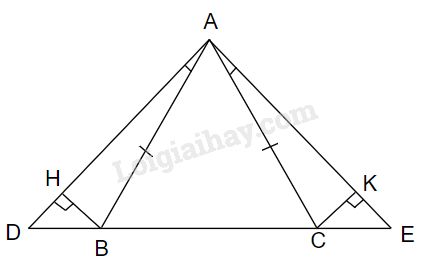
a) \(ΔABC\) cân tại \(A\) nên \(AB=AC,\widehat {ABC} = \widehat {ACB}\) 

\(\widehat {ABC} + \widehat {ABD} = {180^o}\) (hai góc kề bù)

\(\widehat {ACB} + \widehat {ACE} = {180^o}\) (hai góc kề bù)

Mà \(\widehat {ABC} = \widehat {ACB}\) \( \Rightarrow \widehat {ABD} = \widehat {ACE}\)

Xét \(ΔABD\) và \(ΔACE\) có:

\(\widehat {BAD} = \widehat {CAE}\) (gt)

\(AB = AC\) (vì \(ΔABC\) cân tại \(A\))

\(\widehat {ABD} = \widehat {ACE}\) (chứng minh trên)

\(⇒ ΔABD = ΔACE\) (g.c.g)

\(⇒ BD = CE\) (hai cạnh tương ứng).

b) Xét hai tam giác vuông \(BHA\) và \(CKA\) có:

\(\widehat {BHA} = \widehat {CKA} = {90^o}\)

\(\widehat {BAH} = \widehat {CAK}\) (gt)

\(AB = AC\) (vì \(ΔABC\) cân tại \(A\))

\(⇒ ΔBHA = ΔCKA\) (cạnh huyền – góc nhọn)

\(⇒ BH = CK\) (hai cạnh tương ứng).