Bài 23 trang 40 SBT toán 7 tập 2
Giải bài 23 trang 40 sách bài tập toán 7. Cho tam giác ABC trong đó BC là cạnh lớn nhất. a) Vì sao các góc B và C không thể là góc vuông hoặc góc tù? b) Gọi AH là đường vuông góc kẻ từ A đến BC. So sánh AB + AC với BH + CH rồi chứng minh rằng AB + AC > BC.
Đề bài
Cho tam giác \(ABC\) trong đó \(BC\) là cạnh lớn nhất.
a) Vì sao các góc \(B\) và \(C\) không thể là góc vuông hoặc góc tù?
b) Gọi \(AH\) là đường vuông góc kẻ từ \(A\) đến \(BC.\) So sánh \(AB + AC\) với \(BH + CH\) rồi chứng minh rằng \(AB + AC > BC.\)
Phương pháp giải - Xem chi tiết
Sử dụng:
+) Trong một tam giác, cạnh đối diện với góc vuông (hoặc góc tù) là cạnh lớn nhất
+) Đường xiên luôn lớn hơn đường vuông góc.
Lời giải chi tiết
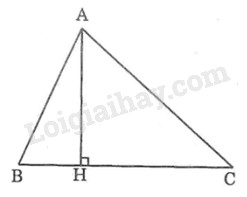
a) Giả sử \(\widehat B \ge 90^\circ\) suy ra \(AC > BC\) (vì trong một tam giác cạnh đối diện với góc vuông hoặc góc tù là cạnh lớn nhất)
Trái giả thiết cạnh \(BC\) là cạnh lớn nhất
Giả sử \(\widehat C \ge 90^\circ \) suy ra \(AB > BC\) (vì trong một tam giác cạnh đối diện với góc vuông hoặc góc tù là cạnh lớn nhất)
Trái với giả thiết \(BC\) là cạnh lớn nhất
Vậy \(\widehat B,\widehat C\) không thể là góc vuông hoặc góc tù hay chúng là các góc nhọn.
b) Ta có điểm \(H\) nằm giữa \(B\) và \(C\) nên \(BH + HC = BC\) (1)
Ta có: \(AB > BH\) (đường xiên lớn hơn đường vuông góc)
\(AC > CH\) (đường xiên lớn hơn đường vuông góc)
Cộng từng vế ta có: \(AB + AC > BH + CH\) (2)
Từ (1) và (2) suy ra: \(AB + AC > BC\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 23 trang 40 SBT toán 7 tập 2 timdapan.com"







