Bài 21 trang 40 SBT toán 7 tập 2
Giải bài 21 trang 40 sách bài tập toán 7. Cho hình 5. Chứng minh rằng MA + MB < IA + IB < CA + CB
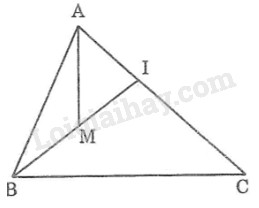
Đề bài
Cho hình 5. Chứng minh rằng \(MA + MB < IA + IB < CA + CB\)
Phương pháp giải - Xem chi tiết
Trong một tam giác:
+) Hiệu độ dài hai cạnh bất kỳ bao giờ cũng nhỏ hơn độ dài cạnh còn lại
+) Độ dài một cạnh bao giờ cũng nhỏ hơn tổng độ dài của hai cạnh còn lại
Chẳng hạn: Trong tam giác \(ABC\), ta có: \(AB - AC < BC < AB + AC.\)
Lời giải chi tiết
Trong \(∆AMI\) ta có:
\( MA < MI + IA\) (bất đẳng thức tam giác)
Cộng vào 2 vế bất đẳng thức với \(MB\) ta có:
\( MA + MB < MI + IA + MB\)
\( \Rightarrow MA + MB < IB + IA \) (1)
Trong \(∆BIC\) ta có:
\(IB < IC + CB\) (bất đẳng thức tam giác)
Cộng vào 2 vế bất đẳng thức với \(IA\) ta có:
\(IB + IA < IC + CB + IA\)
\( \Rightarrow IB + IA < CA + CB\) (2)
Từ (1) và (2) suy ra: \(MA + MB < IB + IA < CA + CB\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 21 trang 40 SBT toán 7 tập 2 timdapan.com"







