Bài 1.54 trang 21 SBT Giải tích 12 Nâng cao

LG a

Khảo sát sự biến thiên và vẽ đồ thị (H) của hàm số

\(y = {{ - x + 3} \over {2x + 1}}\)

Lời giải chi tiết:

+) TXĐ: \(D = \mathbb{R}\backslash \left\{ { - \frac{1}{2}} \right\}\)

+) Chiều biến thiên:

\(y' = \frac{{ - 1 - 3.2}}{{{{\left( {2x + 1} \right)}^2}}} = \frac{{ - 7}}{{{{\left( {x + 1} \right)}^2}}} < 0,\) \(\forall x \in D\)

Hàm số nghịch biến trên mỗi khoảng \(\left( { - \infty ; - \frac{1}{2}} \right)\) và \(\left( { - \frac{1}{2}; + \infty } \right)\).

\(\mathop {\lim }\limits_{x \to  \pm \infty } y =  - \frac{1}{2}\) nên TCN: \(y =  - \frac{1}{2}\)

\(\mathop {\lim }\limits_{x \to {{\left( { - \frac{1}{2}} \right)}^ + }} y =  + \infty ,\mathop {\lim }\limits_{x \to {{\left( { - \frac{1}{2}} \right)}^ - }} y =  - \infty \) nên TCĐ: \(x =  - \frac{1}{2}\).

BBT:

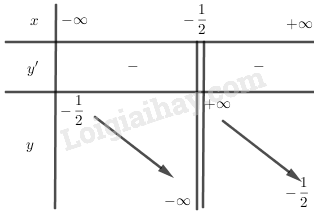
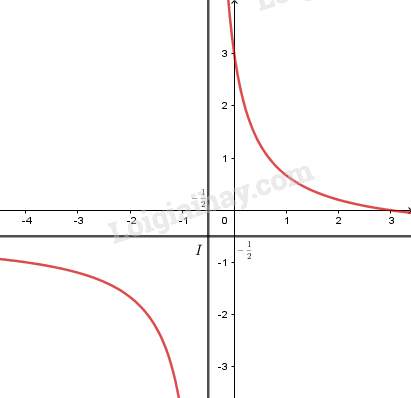
+) Đồ thị:

Cắt trục hoành tại \(\left( {3;0} \right)\), cắt trục tung tại \(\left( {0;3} \right)\).

LG b

Chứng minh rằng với mọi giá trị của m, đường thẳng y = mx + m – 4 luôn đi qua một điểm cố định của đường cong (H)

Lời giải chi tiết:

Gọi \(A\left( {{x_0};{y_0}} \right)\) là điểm cố định mà đường thẳng \(y = mx + m - 4\) luôn đi qua.

Khi đó \({y_0} = m{x_0} + m - 4,\forall m\)

\(\begin{array}{l} \Leftrightarrow m{x_0} + m - 4 - {y_0} = 0,\forall m\\ \Leftrightarrow m\left( {{x_0} + 1} \right) - {y_0} - 4 = 0,\forall m\\ \Leftrightarrow \left\{ \begin{array}{l}{x_0} + 1 = 0\\ - {y_0} - 4 = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{x_0} =  - 1\\{y_0} =  - 4\end{array} \right.\end{array}\)

\( \Rightarrow A\left( { - 1; - 4} \right)\).

Dễ thấy \(A\left( { - 1; - 4} \right) \in \left( H \right)\) vì \(\frac{{ - \left( { - 1} \right) + 3}}{{2.\left( { - 1} \right) + 1}} =  - 4\)

Vậy ta có đpcm.